
THE NUCLEAR FAMILY 1969







 .........
......... .........
.........
|
|
|
|
|
THE RAINBOW LIGHT |
|
|
|
|
|
|
|
3 |
THE |
33 |
15 |
|
|
|
|
|
7 |
RAINBOW |
82 |
37 |
|
|
|
|
|
5 |
LIGHT |
56 |
29 |
|
|
|
|
|
|
|
171 |
81 |
9 |
|
|
1+4 |
|
1+5 |
|
1+7+1 |
8+1 |
|
|
|
|
|
|
|
|
|
|
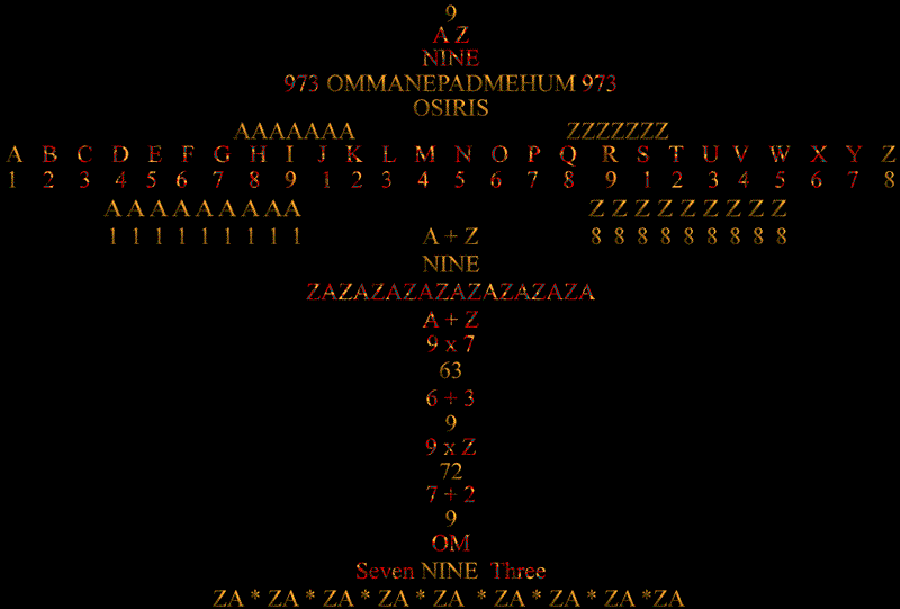

.gif)


|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
18 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
35 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
25 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
|
76 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
48 |
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
55 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
27 |
9 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
10 |
|
133 |
61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
121 |
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
2 |
|
23 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
|
65 |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
First Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3+5 |
|
5+8 |
Add to Reduce |
6+2+6 |
2+6+6 |
5+9 |
|
|
|
|
|
|
|
1+4 |
|
1+8 |
|
|
|
|
|
Second Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
Reduce to Deduce |
1+4 |
1+4 |
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Essence of Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
9 |
|
|
|
|
5 |
6 |
|
|
|
1 |
|
|
|
|
6 |
|
8 |
+ |
= |
|
4+3 |
= |
|
= |
|
= |
|
|
|
|
|
|
|
|
|
8 |
9 |
|
|
|
|
14 |
15 |
|
|
|
19 |
|
|
|
|
24 |
|
26 |
+ |
= |
|
1+1+5 |
= |
|
= |
|
= |
|
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
2 |
3 |
4 |
|
|
7 |
8 |
9 |
|
2 |
3 |
4 |
5 |
|
7 |
|
+ |
= |
|
8+3 |
= |
|
1+1 |
|
= |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
10 |
11 |
12 |
13 |
|
|
16 |
17 |
18 |
|
20 |
21 |
22 |
23 |
|
25 |
|
+ |
= |
|
2+3+6 |
= |
|
1+1 |
|
= |
|
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
+ |
= |
|
3+5+1 |
= |
|
= |
|
= |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
+ |
= |
|
1+2+6 |
= |
|
= |
|
= |
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
1+2 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
1+5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
+ |
= |
|
occurs |
x |
3 |
= |
|
1+8 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
+ |
= |
|
occurs |
x |
3 |
= |
|
2+1 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
8 |
+ |
= |
|
occurs |
x |
3 |
= |
|
2+4 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
9 |
- |
- |
- |
- |
- |
- |
- |
- |
+ |
= |
|
occurs |
x |
2 |
= |
|
1+8 |
|
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4+5 |
|
|
2+6 |
|
1+2+6 |
|
5+4 |
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
OSIRIS |
89 |
35 |
8 |
4 |
ISIS |
56 |
20 |
2 |
3 |
SET |
44 |
8 |
8 |
13 |
Add to Reduce |
189 |
63 |
18 |
1+3 |
Reduce to Deduce |
1+8 |
6+3 |
1+8 |
4 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
81 |
27 |
|
|
|
|
|
|
|
|
45 |
18 |
|
8 |
|
99 |
36 |
9 |
--
RE GODS NAME GODS
RE AS IN THREE IS IS THREE AS IN RE
| 1 |
I |
9 |
9 |
9 |
| 2 |
ME |
18 |
9 |
9 |
| 2 |
EM |
18 |
9 |
9 |
| 1 |
I |
9 |
9 |
9 |
| 3 |
EYE |
35 |
17 |
8 |
| 4 |
EYES |
54 |
18 |
9 |
| 5 |
SIGHT |
63 |
36 |
9 |
| 3 |
SUN |
54 |
9 |
9 |
| 4 |
BALL |
27 |
9 |
9 |
| 5 |
ROUND |
72 |
27 |
9 |
| 4 |
HOOP |
54 |
27 |
9 |
| 4 |
ORBS |
54 |
18 |
9 |
| 7 |
BUBBLES |
63 |
18 |
9 |
| 7 |
SPHERES |
90 |
36 |
9 |
| 7 |
SPHERES |
90 |
36 |
9 |
| 4 |
ORBS |
54 |
18 |
9 |
| 7 |
BUBBLES |
63 |
18 |
9 |
| 5 |
ROUND |
72 |
27 |
9 |
| 4 |
BALL |
27 |
9 |
9 |
| 4 |
HOOP |
54 |
27 |
9 |
| 3 |
SUN |
54 |
9 |
9 |
| 7 |
JUPITER |
99 |
36 |
9 |
| 5 |
WORLD |
72 |
27 |
9 |
| 11 |
SAGITTARIUS |
144 |
45 |
9 |
| 4 |
GAIA |
18 |
9 |
9 |
| 3 |
TAO |
36 |
9 |
9 |
| 4 |
REAL |
36 |
18 |
9 |
| 7 |
REALITY |
90 |
36 |
9 |
| 1 |
I |
9 |
9 |
9 |
| 2 |
ME |
18 |
9 |
9 |
| 3 |
IVE |
36 |
18 |
9 |
| 3 |
EGO |
27 |
18 |
9 |
| 10 |
CONSCIENCE |
90 |
45 |
9 |
| 6 |
DIVINE |
63 |
36 |
9 |
| 7 |
THOUGHT |
99 |
36 |
9 |
| 6 |
SORROW |
108 |
36 |
9 |
| 4 |
LOVE |
54 |
18 |
9 |
| 9 |
FIFTYFOUR |
126 |
54 |
9 |
7 |
LETTERS |
99 |
27 |
9 |
12 |
HIEROGLYPHIC |
135 |
81 |
9 |
8 |
GLYPHICS |
99 |
45 |
9 |
- |
HORUS |
- |
- |
- |
- |
H+O |
23 |
5 |
5 |
- |
R |
18 |
9 |
9 |
- |
U+S |
40 |
13 |
4 |
5 |
|
81 |
27 |
18 |
- |
- |
1+8 |
1+8 |
1+8 |
5 |
|
9 |
9 |
9 |
-
|
PTAH |
- |
- |
- |
- |
P+T |
36 |
9 |
9 |
- |
A+H |
9 |
9 |
9 |
- |
PTAH |
45 |
18 |
18 |
- |
- |
4+5 |
1+8 |
1+8 |
4 |
|
9 |
9 |
9 |
-
|
9+1+8 RAH 8+1+9 |
27 |
18 |
9 |
- |
1+2+3+4 ATUM 4+3+2+1 |
10 |
10 |
1 |
- |
- |
- |
- |
- |
11 |
NOTHINGNESS |
144 |
54 |
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
3 |
NUN |
49 |
13 |
4 |
4 |
NONE |
48 |
21 |
3 |
- |
- |
- |
- |
- |
10 |
NAMES OF GOD |
99 |
36 |
9 |
7 |
THOUGHT |
99 |
36 |
9 |
6 |
DIVINE |
63 |
36 |
9 |
7 |
REALITY |
90 |
36 |
9 |
8 |
MAGNETIC |
72 |
36 |
9 |
5 |
FIELD |
36 |
27 |
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
12 |
|
999 |
999 |
999 |
A
MAZE
IN
ZAZAZA ENTER AZAZAZ
AZAZAZAZAZAZAZZAZAZAZAZAZAZA
ZAZAZAZAZAZAZAZAZAAZAZAZAZAZAZAZAZAZ
THE
MAGICALALPHABET
ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA
12345678910111213141516171819202122232425262625242322212019181716151413121110987654321
A
HISTORY OF GOD
Karen Armstrong 1993
The God of the Mystics
Page 250
"Perhaps the most famous of the early Jewish mystical texts is the fifth century Sefer Yezirah (The Book of Creation). There is no attempt to describe the creative process realistically;
the account is unashamedly symbolic and shows God creating the world by means of language as though he were writing a book. But language has been entirely transformed and the message of creation is no longer clear. Each letter of the Hebrew alphabet is given a numerical value; by
combining the letters with the sacred numbers, rearranging them in
endless configurations, the mystic weaned his mind away from the normal connotations of words."
Page 250
"THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY
THE ACCOUNT IS UNASHAMEDLY SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS
OF LANGUAGE AS THOUGH HE WERE WRITING A BOOK BUT LANGUAGE HAS BEEN ENTIRELY
TRANSFORMED AND THE MESSAGE OF CREATION IS NO LONGER CLEAR EACH LETTER OF THE
HEBREW ALPHABET IS GIVEN A NUMERICAL VALUE BY COMBINING THE LETTERS WITH THE
SACRED NUMBERS REARRANGING THEM IN ENDLESS CONFIGURATIONS THE MYSTIC WEANED
THE MIND AWAY FROM THE NORMAL CONNOTATIONS OF WORDS"
....
THE LIGHT IS RISING NOW RISING IS THE LIGHT
ADVENT 2202 ADVENT
THE
ENGLISH LANGUAGE
TRANSMUTED INTO NUMBER
IS
ONE OF THE MAIN CONDUITS
THROUGH WHICH APPEAR CLEARER UNDERSTANDING
OF
THOSE REFRACTED PATTERNS AND SENSIBILITIES APPARENTLY RANDOM
DESCRIBING ENERGIES WHICH INTERMINGLED WITHIN THE GREAT HERE AND NOW
ARE
CONSIDERED
THE
CREATIVE LIVING EXPERIENCE
OF
REALITY
REAL = 9 9 = REAL
REALITY = 9 9 = REALITY
OUR REALITY = 9 9 = OUR REALITY
3 |
THE |
33 |
15 |
6 |
4 |
MIND |
40 |
22 |
4 |
2 |
OF |
21 |
12 |
3 |
9 |
HUMANKIND |
95 |
41 |
5 |
18 |
First Total |
|
|
|
1+8 |
Add to Reduce |
1+8+9 |
9+0 |
1+8 |
9 |
Second Total |
|
|
|
|
Reduce to Deduce |
1+8 |
- |
- |
|
Essence of Number |
|
|
|

THE
FIELD
THE QUEST FOR THE SECRET FORCE OF THE UNIVERSE
Lynne McTaggart 2001
LIGHT IN THE DARKNESS
PROLOGUE
The Coming Revolution
"WE ARE POISED ON THE brink of a revolution - a revolution as daring.and profound as Einstein's discovery of relativity; At the very frontier of science new ideas are emerging that challenge everything we believe about how our world works and how we define ourselves. Discoveries are being made that prove what religion has always espoused: that human beings are far more extraordinary than an assemblage of flesh and bones. At its most fundamental, this new science answers questions that have perplexed scientists for hundreds of years. At its.most profound, this is a science of the miraculous.
For a number of decades respected scientists in a variety of disciplines all over the world have been carrying out welldesigned ex:perimenfs whose results fly in the face of current, biology and physics together, these studies offer us copious information about the central organizing force governing our bodies and the rest of the cosmos.
What they have discovered is nothing less than astonishing. At our most elemental, we are not a chemical reaction, but an energetic charge. Human beings and all living things are a coalescence of energy in a field of energy connected to every other thing in the world. This pulsating energy field is the / Page XVI / central engine of our being and our consciousness, the alpha and the Omega of our existence.
There is no 'me' and 'not-me' duality to our bodies in relation to the universe, but one underlying energy field. This field is responsible'for our mind's highest functions, the information source guiding the growth of our bodies. It is our brain, our heart, our memory - indeed, a blueprint of the world for all time. The field is the force, rather than germs or genes, that finally determines whether we are healthy or ill, the force which must be tapped in order to heal. We are attached and engaged, indivisible from our world, and our only fundamental truth is our relationship with it, 'The field,' as Einstein once succinctly put it, 'is the only reality.'1"
MIN DOTH DREAM WHAT IN HEAVEN DOTH MIN MEAN
TABOO
Alan Watts
Page 295
Traditional Australian Aborigines believe, as do many other 'primitive' cultures, that rocks, stones and mountains are alive / Page 296 / and that we 'sing' the world into being - that we are creating as we name things. The discoveries of Braud and Jalm showed that this was more than superstition. It was just as the Achuar and the Huaorani Indians believe. On our deepest level, we do share our dreams."
"we 'sing' the world into being - that we are creating as we name things."
SING ME ANOTHER ONE DO
LOOK AT THE 5FIVES LOOK AT THE 5FIVES LOOK AT THE 5FIVES THE 5FIVES THE 5FIVES
ADVENT 2202 ADVENT
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
- |
- |
1+4 |
- |
1+5 |
|
2+1+2 |
7+7 |
2+3 |
6 |
6 |
5 |
|
6 |
THE SWORD OF WORDS |
5 |
14 |
5 |
- |
- |
- |
|
- |
- |
- |
1+4 |
- |
6 |
6 |
5 |
|
6 |
THE SWORD OF WORDS |
5 |
5 |
5 |
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
3 |
|
33 |
15 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
3 |
|
79 |
34 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
3 |
|
21 |
12 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
7 |
|
79 |
34 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
1+5 |
2+4 |
|
|
1+8 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+4 |
- |
1+5 |
|
2+1+2 |
7+7 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+4 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
1+5 |
2+4 |
|
|
1+8 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+4 |
- |
1+5 |
|
2+1+2 |
7+7 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+4 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
1+5 |
2+4 |
|
|
1+8 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+4 |
- |
1+5 |
|
2+1+2 |
7+7 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+4 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
13 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
15 |
THE SWORD OF WORDS |
- |
- |
- |
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
15 |
|
|
|
S |
= |
1 |
- |
5 |
SWORD |
79 |
25 |
7 |
|
|
|
|
1+5 |
2+4 |
|
1+8 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
|
|
|
|
|
|
|
|
W |
= |
5 |
- |
5 |
WORDS |
79 |
25 |
7 |
|
|
|
|
|
|
|
|
- |
- |
14 |
- |
15 |
THE SWORD OF WORDS |
212 |
77 |
23 |
|
|
|
|
|
|
|
|
- |
- |
1+4 |
- |
1+5 |
|
2+1+2 |
7+7 |
2+3 |
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+4 |
- |
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
THE SWORD OF WORDS |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
A |
= |
1 |
- |
9 |
ABCDEFGHI |
45 |
45 |
45 |
|
|
|
|
|
|
|
|
|
|
J |
= |
1 |
- |
9 |
JKLMNOPQR |
126 |
45 |
45 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
8 |
STUVWXYZ |
180 |
45 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
351 |
135 |
126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
B |
= |
2 |
2 |
1 |
B |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
D |
= |
4 |
4 |
1 |
D |
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
I |
= |
9 |
9 |
1 |
I |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
10 |
1 |
|
10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
K |
= |
2 |
11 |
1 |
K |
11 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
M |
= |
4 |
13 |
1 |
M |
13 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
1 |
|
17 |
8 |
|
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
18 |
1 |
R |
18 |
9 |
9 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
19 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
20 |
1 |
T |
20 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
V |
= |
4 |
22 |
1 |
V |
22 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
1 |
|
24 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
1 |
|
25 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
1 |
|
26 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
126 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
- |
- |
1+2+6 |
- |
9 |
ABCDEFGHI |
45 |
45 |
45 |
|
|
|
|
1+2 |
1+5 |
1+8 |
2+1 |
2+4 |
1+8 |
- |
- |
|
- |
9 |
JKLMNOPQR |
126 |
45 |
45 |
|
3 |
|
|
3 |
|
|
|
|
|
- |
- |
|
- |
8 |
STUVWXYZ |
180 |
45 |
36 |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
26 |
ADD TO REDUCE |
351 |
135 |
126 |
|
3 |
|
|
3 |
|
|
|
|
|
- |
- |
|
- |
2+6 |
REDUCE TO DEDUCE |
3+5+1 |
1+3+5 |
1+2+6 |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
8 |
ESSENCE OF NUMBER |
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A |
= |
1 |
- |
ABCDEFGHI |
J |
= |
1 |
- |
JKLMNOPQR |
S |
= |
1 |
- |
STUVWXYZ |
|
|
|
|
|
|
|
|
1 |
|
B |
= |
2 |
2 |
BE |
|
|
|
3 |
|
D |
= |
4 |
4 |
DE |
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
I |
= |
9 |
9 |
I |
|
|
|
10 |
|
K |
= |
2 |
11 |
KA |
|
|
|
12 |
|
M |
= |
4 |
13 |
EM |
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
R |
= |
9 |
18 |
R |
|
|
|
19 |
|
T |
= |
2 |
20 |
TE |
|
|
|
21 |
|
V |
= |
4 |
22 |
VE |
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
126 |
|
|
- |
- |
1+2+6 |
- |
ABCDEFGHI |
- |
- |
|
- |
JKLMNOPQR |
- |
- |
|
- |
STUVWXYZ |
- |
- |
|
- |
ADD TO REDUCE |
- |
- |
|
- |
REDUCE TO DEDUCE |
- |
- |
|
- |
ESSENCE OF NUMBER |
THERE ARE MORE LETTERS OF THE LETTER E IN THE ABOVE VERSION THAN ENOUGH
SEEN THIS WAY ROUND 19 IN ALL
NINETEEN 59552555 NINETEEN
WELL I NEVER DID YOU EVER
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Onomatopoeia (also onomatopeia in American English), is the process of creating a word that phonetically imitates, resembles, or suggests the sound that it describes. Such a word itself is also called an onomatopoeia. Common onomatopoeias include animal noises such as "oink", "meow" (or "miaow"), "roar" and "chirp".
Onomatopoeia - Wikipedia
https://en.wikipedia.org › wiki › Onomatopoeia
Onomatopoeia[note 1] (also onomatopeia in American English), is the process of creating a word that phonetically imitates, resembles, or suggests the sound that it describes. Such a word itself is also called an onomatopoeia. Common onomatopoeias include animal noises such as "oink", "meow" (or "miaow"), "roar" and "chirp". Onomatopoeia can differ between languages: it conforms to some extent to the broader linguistic system;[6][7] hence the sound of a clock may be expressed as "tick tock" in English, "tic tac" in Spanish and Italian (shown in the picture), "di da" in Mandarin, "katchin katchin" in Japanese, or "tik-tik" in Hindi.
Although in the English language the term onomatopoeia means 'the imitation of a sound', the compound word onomatopoeia (???µat?p???a) in the Greek language means 'making or creating names'. For words that imitate sounds, the term ???µ?µ?t??? (echomimetico) or echomimetic) is used. The word ???µ?µ?t??? (echomimetico) derives from "???", meaning 'echo' or 'sound', and "µ?µ?t???", meaning 'mimetic' or 'imitating'.
Further information: List of animal sounds
A bang flag gun, a novelty item
In the case of a frog croaking, the spelling may vary because different frog species around the world make different sounds: Ancient Greek brekekekex koax koax (only in Aristophanes' comic play The Frogs) probably for marsh frogs; English ribbit for species of frog found in North America; English verb croak for the common frog.[8]
Some other very common English-language examples are hiccup, zoom, bang, beep, moo, and splash. Machines and their sounds are also often described with onomatopoeia: honk or beep-beep for the horn of an automobile, and vroom or brum for the engine. In speaking of a mishap involving an audible arcing of electricity, the word "zap" is often used (and its use has been extended to describe non-auditory effects generally connoting the same sort of localized but thorough[clarification needed] interference or destruction similar to that produced in short-circuit sparking).
Human sounds sometimes provide instances of onomatopoeia, as when mwah is used to represent a kiss.[9]
For animal sounds, words like quack (duck), moo (cow), bark or woof (dog), roar (lion), meow/miaow or purr (cat), cluck (chicken) and baa (sheep) are typically used in English (both as nouns and as verbs).
Some languages flexibly integrate onomatopoeic words into their structure. This may evolve into a new word, up to the point that the process is no longer recognized as onomatopoeia. One example is the English word "bleat" for sheep noise: in medieval times it was pronounced approximately as "blairt" (but without an R-component), or "blet" with the vowel drawled, which more closely resembles a sheep noise than the modern pronunciation.
An example of the opposite case is "cuckoo", which, due to continuous familiarity with the bird noise down the centuries, has kept approximately the same pronunciation as in Anglo-Saxon times and its vowels have not changed as they have in the word furrow.
Verba dicendi ("words of saying") are a method of integrating onomatopoeic words and ideophones into grammar.
Sometimes, things are named from the sounds they make. In English, for example, there is the universal fastener which is named for the sound it makes: the zip (in the UK) or zipper (in the U.S.) Many birds are named after their calls, such as the bobwhite quail, the weero, the morepork, the killdeer, chickadees and jays, the cuckoo, the chiffchaff, the whooping crane, the whip-poor-will, and the kookaburra. In Tamil and Malayalam, the word for crow is kaakaa. This practice is especially common in certain languages such as Maori, and so in names of animals borrowed from these languages.
Comics and advertising
A sound effect of breaking a door
Comic strips and comic books make extensive use of onomatopoeia. Popular culture historian Tim DeForest noted the impact of writer-artist Roy Crane (1901–1977), the creator of Captain Easy and Buz Sawyer:
It was Crane who pioneered the use of onomatopoeic sound effects in comics, adding "bam," "pow" and "wham" to what had previously been an almost entirely visual vocabulary. Crane had fun with this, tossing in an occasional "ker-splash" or "lickety-wop" along with what would become the more standard effects. Words as well as images became vehicles for carrying along his increasingly fast-paced storylines.[11]
In 2002, DC Comics introduced a villain named Onomatopoeia, an athlete, martial artist, and weapons expert, who often speaks pure sounds.
Advertising uses onomatopoeia for mnemonic purposes, so that consumers will remember their products, as in Alka-Seltzer's "Plop, plop, fizz, fizz. Oh, what a relief it is!" jingle, recorded in two different versions (big band and rock) by Sammy Davis, Jr.
Rice Krispies (US and UK) and Rice Bubbles (AU)[clarification needed] make a "snap, crackle, pop" when one pours on milk. During the 1930s, the illustrator Vernon Grant developed Snap, Crackle and Pop as gnome-like mascots for the Kellogg Company.
Sounds appear in road safety advertisements: "clunk click, every trip" (click the seatbelt on after clunking the car door closed; UK campaign) or "click, clack, front and back" (click, clack of connecting the seat belts; AU campaign) or "click it or ticket" (click of the connecting seat belt, with the implied penalty of a traffic ticket for not using a seat belt; US DOT (Department of Transportation) campaign).
The sound of the container opening and closing gives Tic Tac its name.
Manner imitation
Main article: Ideophone
In many of the world's languages, onomatopoeic-like words are used to describe phenomena beyond the purely auditive. Japanese often uses such words to describe feelings or figurative expressions about objects or concepts. For instance, Japanese barabara is used to reflect an object's state of disarray or separation, and shiiin is the onomatopoetic form of absolute silence (used at the time an English speaker might expect to hear the sound of crickets chirping or a pin dropping in a silent room, or someone coughing). In Albanian, tartarec is used to describe someone who is hasty. It is used in English as well with terms like bling, which describes the glinting of light on things like gold, chrome or precious stones. In Japanese, kirakira is used for glittery things.
Examples in media
James Joyce in Ulysses (1922) coined the onomatopoeic tattarrattat for a knock on the door.[12] It is listed as the longest palindromic word in The Oxford English Dictionary.[13]
Whaam! (1963) by Roy Lichtenstein is an early example of pop art, featuring a reproduction of comic book art that depicts a fighter aircraft striking another with rockets with dazzling red and yellow explosions.
In the 1960s TV series Batman, comic book style onomatopoeic words such as wham!, pow!, biff!, crunch! and zounds! appear onscreen during fight scenes.
Ubisoft's XIII employed the use of comic book onomatopoeic words such as bam!, boom! and noooo! during gameplay for gunshots, explosions and kills, respectively. The comic-book style is apparent throughout the game and is a core theme, and the game is an adaptation of a comic book of the same name.
The chorus of American popular songwriter John Prine's song "Onomatopoeia" cleverly incorporates onomatopoeic words: "Bang! went the pistol. | Crash! went the window. | Ouch! went the son of a gun. | Onomatopoeia | I don't wanna see ya | Speaking in a foreign tongue."
The marble game KerPlunk has an onomatopoeic word for a title, from the sound of marbles dropping when one too many sticks has been removed.
The Nickelodeon cartoon's title KaBlam! is implied to be onomatopoeic to a crash.
Each episode of the TV series Harper's Island is given an onomatopoeic name which imitates the sound made in that episode when a character dies. For example, in the episode titled "Bang" a character is shot and fatally wounded, with the "Bang" mimicking the sound of the gunshot.
Mad Magazine cartoonist Don Martin, already popular for his exaggerated artwork, often employed comic-book style onomatopoeic "sound effects" in his drawings (for example, "thwizzit" is the sound of a sheet of paper being yanked from a typewriter). Fans have compiled The Don Martin Dictionary, cataloguing each "sound" and its "meaning".
Cross-linguistic examples
Main article: Cross-linguistic onomatopoeias
In linguistics
A key component of language is its arbitrariness and what a word can represent,[clarification needed] as a word is a sound created by humans with attached meaning to said sound.[14] No one can determine the meaning of a word purely by how it sounds. However, in onomatopoeic words, these sounds are much less arbitrary; they are connected in their imitation of other objects or sounds in nature. Vocal sounds in the imitation of natural sounds doesn't necessarily gain meaning, but can gain symbolic meaning.[clarification needed][15] An example of this sound symbolism in the English language is the use of words starting with sn-. Some of these words symbolize concepts related to the nose (sneeze, snot, snore). This does not mean that all words with that sound relate to the nose, but at some level we recognize a sort of symbolism associated with the sound itself. Onomatopoeia, while a facet of language, is also in a sense outside of the confines of language.[16]
In linguistics, onomatopoeia is described as the connection, or symbolism, of a sound that is interpreted and reproduced within the context of a language, usually out of mimicry of a sound.[17] It is a figure of speech, in a sense. Considered a vague term on its own, there are a few varying defining factors in classifying onomatopoeia. In one manner, it is defined simply as the imitation of some kind of non-vocal sound using the vocal sounds of a language, like the hum of a bee being imitated with a "buzz" sound. In another sense, it is described as the phenomena of making a new word entirely.
Onomatopoeia works in the sense of symbolizing an idea in a phonological context, not necessarily constituting a direct meaningful word in the process.[18] The symbolic properties of a sound in a word, or a phoneme, is related to a sound in an environment, and are restricted in part by a language's own phonetic inventory, hence why many languages can have distinct onomatopoeia for the same natural sound. Depending on a language's connection to a sound's meaning, that language's onomatopoeia inventory can differ proportionally. For example, a language like English generally holds little symbolic representation when it comes to sounds, which is the reason English tends to have a smaller representation of sound mimicry then a language like Japanese that overall has a much higher amount of symbolism related to the sounds of the language.
The evolution of language
In ancient Greek philosophy, onomatopoeia was used as evidence for how natural a language was: it was theorized that language itself was derived from natural sounds in the world around us. Symbolism in sounds was seen as deriving from this.[19] Some linguists hold that onomatopoeia may have been the first form of human language.[16]
Role in early language acquisition
When first exposed to sound and communication, humans are biologically inclined to mimic the sounds they hear, whether they are actual pieces of language or other natural sounds.[20] Early on in development, an infant will vary his/her utterances between sounds that are well established within the phonetic range of the language(s) most heavily spoken in their environment, which may be called "tame" onomatopoeia, and the full range of sounds that the vocal tract can produce, or "wild" onomatopoeia.[18] As one begins to acquire one's first language, the proportion of "wild" onomatopoeia reduces in favor of sounds which are congruent with those of the language they are acquiring.
During the native language acquisition period, it has been documented that infants may react strongly to the more wild-speech features to which they are exposed, compared to more tame and familiar speech features. But the results of such tests are inconclusive.
In the context of language acquisition, sound symbolism has been shown to play an important role.[15] The association of foreign words to subjects and how they relate to general objects, such as the association of the words takete and baluma with either a round or angular shape, has been tested to see how languages symbolize sounds.
In other languages
Japanese
Main article: Japanese sound symbolism
The Japanese language has a large inventory of ideophone words that are symbolic sounds. These are used in contexts ranging from day to day conversation to serious news.[21] These words fall into four categories:
Giseigo: mimics humans and animals. (e.g. wanwan for a dog's bark)
Giongo: mimics general noises in nature or inanimate objects. (e.g. zaazaa for rain on a roof)
Gitaigo: describes states of the external world
Gijogo: describes psychological states or bodily feelings.
The two former correspond directly to the concept of onomatopoeia, while the two latter are similar to onomatopoeia in that they are intended to represent a concept mimetically and performatively rather than referentially, but different from onomatopoeia in that they aren't just imitative of sounds. For example, "shiinto" represents something being silent, just as how an anglophone might say "clatter, crash, bang!" to represent something being noisy. That "representative" or "performative" aspect is the similarity to onomatopoeia.
Sometimes Japanese onomatopoeia produces reduplicated words.[19]
Hebrew
As in Japanese, onomatopoeia in Hebrew sometimes produces reduplicated verbs:[22]:208
???? shikshék "to make noise, rustle".[22]:207
???? rishrésh "to make noise, rustle".[22]:208
Malay
There is a documented correlation within the Malay language of onomatopoeia that begin with the sound bu- and the implication of something that is rounded, as well as with the sound of -lok within a word conveying curvature in such words like lok, kelok and telok ('locomotive', 'cove', and 'curve' respectively).[23]
Arabic
The Qur'an, written in Arabic, documents instances of onomatopoeia.[16] Of about 77,701 words, there are nine words that are onomatopoeic: three are animal sounds (e.g., "mooing"), two are sounds of nature (e.g.; "thunder"), and four that are human sounds (e.g., "whisper" or "groan").
Albanian
There is wide array of objects and animals in the Albanian language that have been named after the sound they produce. Such onomatopoeic words are shkrepse (matches), named after the distinct sound of friction and ignition of the match head; take-tuke (ashtray) mimicking the sound it makes when placed on a table; shi (rain) resembling the continuous sound of pouring rain; kukumjaçkë (Little owl) after its "cuckoo" hoot; furçë (brush) for its rustling sound; shapka (slippers and flip-flops); pordhë (rumorous flatulence) and fëndë (silent flatulence).
Urdu
In Urdu, onomatopoeic words like bak-bak, churh-churh are used to indicate a silly talk. Other examples of onomatopoeic words being used to represent actions are fatafat (to do something fast), dhak-dhak (to represent fear with the sound of fast beating heart), tip-tip (to signify a leaky tap) etc. Movement of animals or objects is also sometimes represented with onomatopoeic words like bhin-bhin (for a housefly), sar-sarahat (the sound of a cloth being dragged on or off a furniture) etc.
See also
Anguish Languish
Japanese sound symbolism
List of animal sounds
List of onomatopoeias
Sound mimesis in various cultures
Sound symbolism
Vocal learning
1 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 1
2 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 2
3 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 3
4 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 4
5 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 5
6 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 6
7 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 7
8 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 8
9 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 9
10 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 10
11 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 11
12 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 14
13 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 4
14 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 14
15 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 15
16 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 16
17 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 17
18 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 18
19 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 19
20 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 20
21 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 21
22 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 22
23 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 23
24 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 24
25 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 25
26 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 26
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
T |
= |
2 |
- |
3 |
|
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
2 |
- |
Q |
= |
8 |
- |
5 |
|
61 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
3 |
- |
B |
= |
2 |
- |
5 |
|
72 |
27 |
9 |
|
|
|
|
|
|
|
|
|
|
4 |
- |
F |
= |
6 |
- |
3 |
|
45 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
5 |
- |
J |
= |
1 |
- |
5 |
|
79 |
16 |
7 |
|
|
|
|
|
|
|
|
|
|
6 |
- |
O |
= |
6 |
- |
4 |
|
60 |
24 |
6 |
|
|
|
|
|
|
|
|
|
|
7 |
- |
T |
= |
2 |
- |
3 |
|
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
8 |
- |
L |
= |
3 |
- |
4 |
|
64 |
19 |
1 |
|
|
|
|
|
|
|
|
|
|
9 |
- |
D |
= |
4 |
- |
3 |
|
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
45 |
|
- |
- |
34 |
- |
35 |
Add |
|
|
|
|
|
|
|
|
|
|
|
|
|
4+5 |
|
- |
|
3+4 |
|
3+5 |
Reduce |
4+7+3 |
1+7+6 |
5+9 |
|
|
|
|
|
|
1+8 |
1+4 |
|
1+8 |
9 |
- |
- |
|
|
|
|
Deduce |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
|
Produce |
1+4 |
1+4 |
1+4 |
|
|
|
|
|
|
|
|
|
|
9 |
- |
- |
- |
7 |
- |
8 |
Essence |
|
|
|
|
|
|
|
|
|
|
|
|
|
The quick brown fox jumps over the lazy dog - Wikipedia ...
From Wikipedia, the free encyclopedia
"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet.
"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet. It is used to show fonts and to test typewriters and computer keyboards, and in other applications involving all of the letters in the English alphabet. Owing to its brevity and coherence, it has become widely known
1 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 1
2 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 2
3 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 3
4 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 4
5 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 5
6 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 6
7 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 7
8 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 8
9 THE QU9CK B9OWN FOX JUMPS OVE9 THE LAZY DOG 9
10 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 10
11 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 11
12 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 12
13 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 13
14 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 14
15 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 15
16 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 16
17 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 17
18 THE QU9CK B9OWN FOX JUMPS OVE9 THE LAZY DOG 18
19 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 19
20 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 20
21 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 21
22 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 22
23 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 23
24 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 24
25 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 25
26 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 26
The quick brown fox jumps over the lazy dog - Wikipedia ...
From Wikipedia, the free encyclopedia
"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet.
"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet. It is used to show fonts and to test typewriters and computer keyboards, and in other applications involving all of the letters in the English alphabet. Owing to its brevity and coherence, it has become widely known
History[edit]
The earliest known appearance of the phrase is from The Michigan School Moderator, a journal that provided many teachers with education-related news and suggestions for lessons.[1] In an article titled "Interesting Notes" in the March 14, 1885 issue, the phrase is given as a suggestion for writing practice: "The following sentence makes a good copy for practice, as it contains every letter of the alphabet: 'A quick brown fox jumps over the lazy dog.'"[2] Note that the phrase in this case begins with the word "A" rather than "The". Several other early sources also use this variation.
As the use of typewriters grew in the late 19th century, the phrase began appearing in typing and stenography lesson books as a practice sentence. Early examples of publications which used the phrase include Illustrative Shorthand by Linda Bronson (1888),[3] How to Become Expert in Typewriting: A Complete Instructor Designed Especially for the Remington Typewriter (1890),[4] and Typewriting Instructor and Stenographer's Hand-book (1892). By the turn of the 20th century, the phrase had become widely known. In the January 10, 1903, issue of Pitman's Phonetic Journal, it is referred to as "the well known memorized typing line embracing all the letters of the alphabet".[5] Robert Baden-Powell's book Scouting for Boys (1908) uses the phrase as a practice sentence for signaling.[6]
The first message sent on the Moscow–Washington hotline was the test phrase "THE QUICK BROWN FOX JUMPED OVER THE LAZY DOG'S BACK 1234567890".[7] Later, during testing, the Russian translators sent a message asking their American counterparts "What does it mean when your people say 'The quick brown fox jumped over the lazy dog?'"[8]
During the 20th century, technicians tested typewriters and teleprinters with repeated lines of "THE QUICK BROWN FOX..." sentence.[9]
THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
T |
= |
2 |
- |
3 |
|
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
2 |
- |
Q |
= |
8 |
- |
5 |
|
61 |
25 |
7 |
|
|
|
|
|
|
|
|
|
|
3 |
- |
B |
= |
2 |
- |
5 |
|
72 |
27 |
9 |
|
|
|
|
|
|
|
|
|
|
4 |
- |
F |
= |
6 |
- |
3 |
|
45 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
5 |
- |
J |
= |
1 |
- |
5 |
|
79 |
16 |
7 |
|
|
|
|
|
|
|
|
|
|
6 |
- |
O |
= |
6 |
- |
4 |
|
60 |
24 |
6 |
|
|
|
|
|
|
|
|
|
|
7 |
- |
T |
= |
2 |
- |
3 |
|
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
8 |
- |
L |
= |
3 |
- |
4 |
|
64 |
19 |
1 |
|
|
|
|
|
|
|
|
|
|
9 |
- |
D |
= |
4 |
- |
3 |
|
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
45 |
|
- |
- |
34 |
- |
35 |
Add |
|
|
|
|
|
|
|
|
|
|
|
|
|
4+5 |
|
- |
|
3+4 |
|
3+5 |
Reduce |
4+7+3 |
1+7+6 |
5+9 |
|
|
|
|
|
|
1+8 |
1+4 |
|
1+8 |
9 |
- |
- |
|
|
|
|
Deduce |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
|
Produce |
1+4 |
1+4 |
1+4 |
|
|
|
|
|
|
|
|
|
|
9 |
- |
- |
- |
7 |
- |
8 |
Essence |
|
|
|
|
|
|
|
|
|
|
|
|
|
THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
17 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
24 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
22 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
26 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
25 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
- |
35 |
First Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3+4 |
|
3+5 |
Add to Reduce |
4+7+3 |
1+7+6 |
5+9 |
|
|
|
1+2 |
1+2 |
2+5 |
3+6 |
2+1 |
3+2 |
2+7 |
|
|
|
|
|
Second Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
Reduce to Deduce |
1+4 |
1+4 |
1+4 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
- |
8 |
Essence of Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
22 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
24 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
25 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
17 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
26 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
- |
35 |
First Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3+4 |
|
3+5 |
Add to Reduce |
4+7+3 |
1+7+6 |
5+9 |
|
|
|
1+2 |
1+2 |
2+5 |
3+6 |
2+1 |
3+2 |
2+7 |
|
|
|
|
|
Second Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
Reduce to Deduce |
1+4 |
1+4 |
1+4 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
- |
8 |
Essence of Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
PANGRAM = 7 = PANGRAM
- |
- |
- |
- |
7 |
PANGRAM |
- |
- |
- |
P |
= |
7 |
- |
1 |
P |
16 |
7 |
7 |
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
N |
= |
5 |
- |
1 |
N |
14 |
5 |
5 |
G |
= |
7 |
- |
1 |
G |
7 |
7 |
7 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
- |
- |
34 |
- |
7 |
PANGRAM |
70 |
34 |
34 |
- |
- |
3+4 |
- |
1+5 |
|
7+0 |
3+4 |
3+4 |
- |
- |
7 |
|
6 |
PANGRAM |
7 |
7 |
7 |
What sentence contains all the letters of the alphabet?
Everybody knows one or two pangrams (sentences that use every letter of the alphabet). You've probably seen some of these before: The quick brown fox jumps over a lazy dog. Pack my box with five dozen liquor jugs.
Big on the Internet
Sentences That Contain Every Letter of the Alphabet
by Robert Quigley ( ) | Thursday, August 5th 2010 at 4:23 pm
A pangram, or holoalphabetic sentence, is a sentence that contains every letter of the alphabet at least once. The most famous pangram is probably the thirty-five-letter-long “The quick brown fox jumps over the lazy dog,” which has been used to test typing equipment since at least the late 1800s.
Pangrams are an important tool for testing typing equipment and compactly showing off every letter of a typeface; trying to pack every letter into as short a sentence as possible is also a sort of sport among linguists and puzzle-solvers.
Here are a few that are famous or otherwise cool:
● “Sphinx of black quartz, judge my vow”: Used by Adobe InDesign to display font samples. (29 letters)
●”Jackdaws love my big sphinx of quartz”: Similarly, used by Windows XP for some fonts. (31 letters)
●”Pack my box with five dozen liquor jugs”: According to Wikipedia, this one is used on NASA’s Space Shuttle. (32 letters)
●”The quick onyx goblin jumps over the lazy dwarf”: Flavor text from an Unhinged Magic Card. (39 letters)
●”Cwm fjord bank glyphs vext quiz”: Amazingly, this 26-word-long sentence uses every letter only once, though it uses some pretty archaic words; translates to “Carved symbols in a mountain hollow on the bank of an inlet irritated an eccentric person.”
●”How razorback-jumping frogs can level six piqued gymnasts!”: Not going to win any brevity awards at 49 letters long, but old-time Mac users may recognize it.
●”Cozy lummox gives smart squid who asks for job pen”: A 41-letter tester sentence for Mac computers after System 7.
A few others we like: “Amazingly few discotheques provide jukeboxes”; “‘Now fax quiz Jack!’ my brave ghost pled”; “Watch Jeopardy!, Alex Trebek’s fun TV quiz game.”
(via Wikipedia; title image via woot.)
Pangram - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Pangram
... pangram. An example is the phrase "Cwm fjord bank glyphs vext quiz" (cwm, a loan word from Welsh, means a steep-sided valley, particularly in Wales).
Pangram
From Wikipedia, the free encyclopedia
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (September 2013)
English language pangram in Baskerville font.
A Pangram (Greek: παν γράμμα, pan gramma, "every letter") or holoalphabetic sentence for a given alphabet is a sentence using every letter of the alphabet at least once. Pangrams have been used to display typefaces, test equipment, and develop skills in handwriting, calligraphy, and keyboarding.
The best known English pangram is "The quick brown fox jumps over the lazy dog." It has been used since at least the late 19th century, was utilized by Western Union to test Telex / TWX data communication equipment for accuracy and reliability, and is now used by a number of computer programs (most notably the font viewer built into Microsoft Windows) to display computer fonts.
An example in another language is the German Victor jagt zwölf Boxkämpfer quer über den großen Sylter Deich, containing all letters used in German, including every umlaut (ä, ö, ü) plus the ß. It has been used since before 1800.
Short pangrams in English are more difficult to come up with and tend to use uncommon words, because the English language uses some letters (especially vowels) much more frequently than others. Longer pangrams may afford more opportunity for humor, cleverness, or thoughtfulness.[1] In a sense, the pangram is the opposite of the lipogram, in which the aim is to omit one or more letters. A perfect pangram contains every letter of the alphabet only once and can be considered an anagram of the alphabet; it is the shortest possible pangram. An example is the phrase "Cwm fjord bank glyphs vext quiz" (cwm, a loan word from Welsh, means a steep-sided valley, particularly in Wales).
Contents [hide]
1 Logographic scripts
2 Self-enumerating pangrams
3 Pangrams in literature
4 See also 4.1 Pangram lists
5 References
Logographic scripts[edit]
Logographic scripts, that is, writing systems composed principally of logograms, cannot be used to produce pangrams in the literal sense, since they are radically different from alphabets or other phonetic writing systems. In such scripts, the total number of signs is large and imprecisely defined, so producing a text with every possible sign is impossible. However, various analogies to pangrams are feasible, including traditional pangrams in a romanization. In Japanese, although typical orthography uses kanji (logograms), pangrams are instead required to contain every kana (syllabic character) when written out in kana alone: the Iroha is a classic example.
In addition, it is possible to create pangrams that demonstrate certain aspects of logographic characters.
Chinese: The Thousand Character Classic is a 1000-character poem in which each character is used exactly once, but it does not include all Chinese characters.
The single character 永 (permanence) incorporates every basic stroke used to write Chinese characters exactly once, as described in the Eight Principles of Yong.
Self-enumerating pangrams[edit]
A self-enumerating pangram is a pangrammatic autogram, or a sentence that inventories its own letters, each of which occurs at least once. The first ever example was produced by Rudy Kousbroek, a Dutch journalist and essayist, who publicly challenged Lee Sallows, a British recreational mathematician resident in the Netherlands, to produce an English translation of his Dutch pangram. In the sequel, Sallows built an electronic "pangram machine", that performed a systematic search among millions of candidate solutions. The machine was successful in identifying the following 'magic' translation:[2][3][4]
This pangram contains four As, one B, two Cs, one D, thirty Es, six Fs, five Gs, seven Hs, eleven Is, one J, one K, two Ls, two Ms, eighteen Ns, fifteen Os, two Ps, one Q, five Rs, twenty-seven Ss, eighteen Ts, two Us, seven Vs, eight Ws, two Xs, three Ys, & one Z.
Other approaches have been taken to find self-enumerating pangrams, too. Chris Patuzzo, a British computer scientist was able to reduce the problem of finding a self-enumerating pangram to the Boolean satisfiability problem. He did this by using a bespoke Hardware description language as a stepping stone and then applied the Tseitin transformation to the resulting chip.[5]
Pangrams in literature[edit]
Pangram "The quick brown fox..." and searches of a shorter pangram are the cornerstone of a plot of the novel by Mark Dunn "Ella Minnow Pea".[6] Search successfully comes to the end with finding "Pack my box with five dozen liquor jugs".
The Evolution of Writing, Reading and Printing of the Alphabet
History of the Latin Alphabet
Latin or Roman script is a series of graphic representative signs (script) based on the letters of the classical Latin alphabet, and derived from a form of the Cumaean Greek version of the Greek alphabet, used by the Etruscans.
The Latin script is the most widely used alphabetic writing system in the world. It is the standard script of the English language and is frequently referred to simply as ‘the alphabet’ in both spoken and written English.
It is a true alphabet (As in, it contains separate letters [not diacritic marks] for both consonants and vowels) which originated in the 7th century BC in Italy and has changed continually over the last 2500 years. It also has roots in the Semitic alphabet and its offshoot alphabets, the Phoenician, Greek, and Etruscan.
NOTE: The Semitic alphabet in its earliest form, the Proto-Sinaitic script of Egypt has yet to be fully deciphered. The earliest known alphabetic (or ‘proto-alphabetic’) inscriptions are written in the so-called Proto-Sinaitic (or Proto-Canaanite) script sporadically attested as being in use across the Sinai Peninsula in Egypt and in Canaan (the latter corresponds roughly to present-day Lebanon, Jordan, Syria and Israel, a land also known as Phoenicia) during the Middle and Late Bronze Age. However, the script did not become widely used until the rise of what were dubbed new Semitic kingdoms in the 13th and 12th centuries BC.
The Phoenician alphabet is a direct continuation of the ‘Proto-Canaanite’ script of the Bronze Age collapse period which overall spanned 3000 BC to 1200 BC, but varied in length between Europe, the Near East and South Asia. The Ahiram epitaph, engraved on the sarcophagus of king Ahiram from about 1200 BC, one of five known Byblian royal inscriptions, shows what is essentially the fully developed Phoenician script.
Over time, the phonetic sound values of some letters changed, some letters were lost and others gained, and several writing styles (‘hands’) developed. Two styles, the minuscule and majuscule hands, were ultimately combined into one script with alternate forms for the lower and upper case letters. Due to classicism, modern uppercase letters differ only slightly from their classical counterparts. There are few regional variants.
The Latin alphabet started out as uppercase serifed (with a slight projection finishing off a stroke of a letter) letters known as roman square capitals. Also known as capitalis monumentalis, inscriptional capitals, elegant capitals and capitalis quadrata, this ancient Roman form of writing, became and still is the basis for modern capital letters.
Meanwhile, the lowercase letters evolved through cursive styles (where some characters are written joined together in a flowing manner, generally for the purpose of making writing faster i.e. what the English refer to as longhand). These styles were fundamentally developed in order to adapt the formerly inscribed alphabet to be written with a pen.
Down through the ages, many dissimilar stylistic variants of each letter have appeared but remain identified as the same original letter. Following the evolution of the *dab* alphabet from the Western Greek Alphabet through Old Italic alphabet, G developed from C, the letter J developed from a flourished I, V and U split and the ligature of VV became W, the letter thorn was introduced from the runic alphabet but was lost in all languages except Icelandic, and the letter s could be written either as a long s (ſ) inside a word or as a terminal s at the end or after a long s (ß) after the 7th century AD, but the long s was generally abandoned in the 19th century.
However, courtesy of classical revival, Roman capitals were reintroduced by humanists making Latin inscriptions easily legible to modern readers while many medieval manuscripts are unreadable to an untrained modern reader, due to unfamiliar letterforms, narrow spacing and abbreviation marks with some exceptions of some marks such as the apostrophe and the exception of Carolingian minuscule letters (lower caps) which were mistaken for Roman.
Additionally the phonetic value of the letters has changed from the original and is certainly not constant across the languages adopting the Latin alphabet, for instance comparing English with French. Quite often the orthography fails to fully match the phonetics, resulting in Homophonic heterographs (words written differently but sounding the same) for example in English rough and ruff and also adopting digraphs covering new sounds, such as ‘sh’ for Voiceless post-alveolar fricative in English.
Development of Letter case within the Latin Alphabet
Letter case (often simply referred to as case) is the distinction between the letters of the alphabet that are written in their larger form known as upper case (however other terms frequently used are uppercase, capital letters, capitals, caps, large letters, or more formally majuscule). In logical contrast the smaller version of letters are known as lower case (other terms regularly in use include lowercase, small letters, along with the more formal minuscule). Both only apply in the written representation of certain languages.
The writing systems that physically distinguish between the upper and lower case employ two parallel sets of letters, where each letter in one set normally has an equivalent in the other set. Fundamentally, the two case variants are alternative presentations of the same letter; they are both assigned the same name as well as pronunciation and have identical values when information is to be sorted in alphabetical order.
The terms upper case and lower case maybe be written as two consecutive words, connected with a hyphen (upper-case and lower-case), or the two components merged as a single word (uppercase and lowercase). In fact, these terms originated from what were the common layouts of the shallow drawers called type cases used to hold the movable type for letterpress printing. Traditionally, the capital letters were stored in a separate shallow tray or ‘case’ that was located above the case which held the small letters, and since capital letters are taller the name proved easy to remember.
Majuscule, is technically any script in which the letters are depicted with very few or short ascenders and descenders, or none at all (for example, the majuscule scripts used in the Codex Vaticanus Graecus 1209, or the Book of Kells). By virtue of their visual impact, this then made the term majuscule an apt descriptor for what much later came to be more commonly referred to as uppercase or capital letters.
The Codex Vaticanus, author Eusebius was completed between 300 and 325 is considered to be one of the oldest extant manuscripts of the Greek Bible (Old and New Testament), and one of the four great uncial codices. The Codex is named after its place of conservation in the Vatican Library, where it has been kept since at least the 15th century.
The Book of Kells (Latin: Codex Cenannensis; Irish: Leabhar Cheanannais is held in Dublin, Trinity College Library in Ireland. Sometimes known as the Book of Columba, it is an illuminated manuscript Gospel book in Latin, containing the four Gospels of the New Testament together with various prefatory texts and tables.
Minuscule refers to lower-case letters. The word is often spelled miniscule, because of its association with the unrelated word miniature and the prefix mini-. Traditionally this has been regarded as a spelling mistake (since minuscule is derived from the word minus), however it is now so common that some dictionaries tend to accept it as a nonstandard or variant spelling. Nevertheless, Miniscule is still less likely to be used in reference to lower-case letters.
Originally alphabets were written entirely in majuscule or capital letters, spaced between well-defined upper and lower bounds. When written quickly with a pen, these tended to result in rounder and much simpler forms. It is from these that the first minuscule writing hands developed, the half-uncials and cursive minuscule, which no longer stayed bound between a pair of lines. These in turn formed the foundations for the Carolingian minuscule script, developed by famous scholar Alcuin of York for use in the court of Charlemagne (742 to 814 AD), which quickly spread across Europe. The advantage of the minuscule over majuscule was supposedly improved, faster readability.
In Latin, papyri from Herculaneum dating before 79 AD (when the ancient Roman town was destroyed by the eruption of Mount Vesuvius) have been found written in old Roman cursive, where the early forms of minuscule letters d’, ‘h’ and ‘r’ for example, can already be recognised. According to papyrologist Knut Kleve, ‘The theory, then, that the lower-case letters have been developed from the fifth century uncials and the ninth century Carolingian minuscules seems to be wrong’. Both majuscule and minuscule letters existed, but the difference between the two variants was initially stylistic rather than orthographic and the writing system was still basically unicameral (of a single legislative body): a given handwritten document could make use of either one style or the other but these were not mixed. European languages did not make the distinction between cases, other than Ancient Greek and Latin until around 1300.
The timeline for writing in Western Europe is divisible into four eras:
Greek majuscule (9th to 3rd century BC) in contrast to the Greek uncial script (3rd century BC to 12th century AD) and the later Greek minuscule
Roman majuscule (7th century BC to 4th century AD) in contrast to the Roman uncial (4th to 8th century AD), Roman Half Uncial, and minuscule
Carolingian majuscule (4th to 8th century AD) in contrast to the Carolingian minuscule (around 780 to 12th century). [Carolingian Empire Franks & Lombards].
Gothic majuscule (13th and 14th century), in contrast to the early Gothic (end of 11th to 13th century), Gothic (14th century), and late Gothic (16th century) minuscules.
NOTE: Uncial is defined as ‘of or written in a majuscule script with rounded unjoined letters which is found in European manuscripts between the 4th and 8th centuries; from which modern capital letters are derived’.
Traditionally, certain letters were rendered differently according to a set of rules. Specifically, those letters that began sentences or nouns were enlarged and often written in a distinct script. There was actually no fixed capitalisation system until the early 18th century. The English language eventually dropped the rule for nouns, while the German language retained it.
Similar evolution has taken place in other alphabets. The lower-case script for the Greek alphabet has its origins in the 7th century and only acquired its quadrilinear form in the 8th century. Over time, uncial letter forms were increasingly mixed into the script. The earliest dated Greek lower-case text is found in the Uspenski Gospels (MS 461 a New Testament minuscule manuscript written in Greek) in the year 835. The modern practice of capitalising the first letter of every sentence appears to have been imported (even today the system is rarely used when printing Ancient Greek materials).
The Evolution of Word Spacing and Punctuation
Modern English, both hand written and printed, uses a space to separate individual words, however not all languages adhere to this practice. In chronological terms spaces were not used to separate words in Latin until roughly 600 to 800 AD, whereas Ancient Hebrew and Arabic did use physical spaces, but partly to compensate for clarity issues arising from the lack of vowels. Traditionally, all CJK languages have had no spaces, and certainly in the main both modern Chinese and Japanese do not; yet conversely modern Korean does use spaces.
Meanwhile, Runic texts make use of either interpunct-like (consisting of a vertically centred dot) or colon-style punctuation marks as word separation devices.
Taking spacing a stage further, essentially it is only those languages based upon a Latin-derived alphabet (English being one) which have adopted a varied methodology of sentence spacing since the advent of movable printing type in the 15th century.
Spacing toward Punctuation
What are known as the Semitic languages (Hebrew, Aramaic, Arabic, and Syriac), especially when written without vowels, were pretty much always recorded with word separation, even in their most ancient form, and indeed continued to be transcribed with this formatting into modern times
The earliest alphabetic based writing had no capitalisation, spaces or vowels and few punctuation marks. However, this system only worked effectively if the subject matter was confined to a limited spread of everyday topics (e.g. written records pertaining to business transactions). Although in real historical terms, punctuation was designed as an aid to reading aloud.
The oldest known document using punctuation is the Mesha Stele (a 9th century BC inscribed stone, set up around 840 BC by King Mesha of Moab Mesha). Mesha Stele is inscribed with the cautionary tale of how Chemosh, the god of Moab, had been angry with his people and as a result allowed them to be subjugated by Israel, but eventually Chemosh returns and helps the people to restore Moab’s independence and throw off the yoke of Israeli oppression. It is written in the Phoenician alphabet and employs points between the words along with horizontal strokes between the sense sections, as punctuation.
The Arrival of Symbolic Punctuation
Most texts of the time were still written in scriptura continua, meaning without any separation between words. However, the Greeks began to sporadically use punctuation marks, consisting of vertically arranged dots [usually two (dicolon) or three (tricolon)], in and around the 5th century b.c. as an aid to the oral delivery of texts. Greek playwrights such as Euripides and Aristophanes definitely used symbols to distinguish the ends of phrases in written drama: essentially helping the thespians to know when to pause. Post 200 b.c., the Greeks used the Aristophanes of Byzantium system (named théseis) of a single dot (punctus) placed at varying heights to mark up speeches at rhetorical dividing lines:
· hypostigmḗ – a low punctus on the baseline to mark off a komma (unit smaller than a clause [a unit of grammatical organisation next below the sentence in rank and in traditional grammar said to consist of a subject and predicate.]);
· stigmḕ mésē – a punctus at midheight to mark off a clause (kōlon); and
· stigmḕ teleía – a high punctus to mark off a sentence (periodos).
In addition, the Greeks used the paragraphos (or gamma) to mark the beginning of sentences, marginal diples (marks once used in margins to draw attention to something in the text.) to mark quotations, and a koronis (both a textual symbol and a mark over vowel letters in Ancient Greek) to indicate the end of major sections.
Circa 1st century b.c., the Romans also occasionally used symbols to indicate pauses, but the Greek théseis, subsequently known by the name distinctiones, prevailed to become a more or less widespread standard from the 1st to the 4th century A.D. Certainly, according to scholarly observer practitioners ranging from Aelius Donatus (Roman grammarian and teacher of rhetoric 1st Century AD) through to Isidore of Seville (Scholar and Archbishop of Seville 7th century AD).
Also, during the 1st century BC, texts were sometimes laid out per capitula, where every sentence had its own separate line. Originally diples were used for these demarcations; however by the late period (664 BC until 332 BC) they had often regressed into comma-shaped marks.
The Development of Punctuation
Punctuation evolved dramatically as copies of the Bible began to be produced in large numbers. Given that it was essential that the holy tome be read aloud, so the copyists began to introduce a range of spoken word marks to help the reader. These included indentation, various punctuation marks (diple, paragraphos, simplex ductus), and an early version of initial capitals (litterae notabiliores).
Jerome (tutored by the aforementioned Aelius Donatus) who along with colleagues, made a translation of the Bible into Latin, the Vulgate around 400 AD, employed a formatting system based on the established methodology used for teaching the speeches of Demosthenes and Cicero. Under this layout per cola et commata every sense-unit was indented and given its own line. However, this layout was solely used for biblical manuscripts in a period covering the 5th to 9th centuries and was then abandoned in favour of punctuation.
Meanwhile in the 7th and 8th centuries Irish and Anglo-Saxon scribes, whose native languages were not derived from Latin, added further visual cues to render texts more intelligible. Irish scribes introduced the practice of word separation. Likewise, insular scribes (post-Roman Hiberno/Saxon) adopted the distinctiones system while adapting it for minuscule script (to make the signage more prominent) not by employing differing height but rather a variable number of marks mainly aligned horizontally (or sometimes triangularly) to indicate a pause's value: one mark for a minor pause, two for the medium version, and three for a major. Most common were the punctus, a comma-shaped mark, and a 7-shaped mark (comma positura), often used in combination. The same symbols could be used in the margin to mark off quotations.
Nevertheless, despite these advances, an alternative system emerged in France during the late 8th century under the Carolingian dynasty. In its original form, this system was used to indicate how the voice should be modulated when chanting the liturgy, but gradually the positurae as it was known, steadily migrated into any text meant to be read aloud, and ultimately to all manuscripts.
Positurae first worked itself into England over the latter part of the 10th century AD, most likely during the Benedictine reform movement, but was not adopted as standard practice until after the Norman Conquest. The original positurae were the punctus, punctus elevatus (an inverted latter day semi-colon), punctus versus, and punctus interrogatives (dot with a flourish above as in the modern day question mark), but a fifth symbol, the punctus flexus (very similar to the punctus interrogatives), was added in the 10th century to indicate a pause of a value between the punctus and punctus elevatus. In the late 11th/early 12th century the punctus versus (similar in appearance to a semicolon) faded away and was taken over by the simple punctus (now with two distinct values).
The arrival of the late Middle Ages saw the addition of the virgula suspensiva (slash or slash with a midpoint dot) which was often used in conjunction with the punctus for different types of pauses. Direct quotations continued to be marked with marginal diples, as they were in antiquity, but from at least the 12th century scribes also began entering diples (sometimes doubled up) within the physical column of text.
Later Developments Leading to Modern Punctutation
The volume of printed material becoming available and thus its readership began to increase after the invention of moveable type in Europe in the 1450s. To quote writer and editor, Lynne Truss, ‘The rise of printing in the 14th and 15th centuries meant that a standard system of punctuation was urgently required.’
The introduction of a standard system of punctuation has also been attributed to the Venetian printers Aldus Manutius (Venetian humanist, scholar, educator, who became a printer and publisher when he helped found the Aldine Press in Venice, 1495) and his grandson. They have been credited with popularising the practice of ending sentences with the colon or full stop, inventing the semicolon (although the punctus versus was still visible in the early 12th century), making occasional use of parentheses and creating the modern comma by lowering the virgule. By 1566, Aldus Manutius the Younger was able to declare that the main objective of punctuation was the clarification of syntax.
In a 19th-century manual of typography, published by American Printer Thomas MacKellar in 1866, he writes:
‘Shortly after the invention of printing, the necessity of stops or pauses in sentences for the guidance of the reader produced the colon and full point. In process of time, the comma was added, which was then merely a perpendicular line, proportioned to the body of the letter. These three points were the only ones used until the close of the fifteenth century, when Aldo Manuccio gave a better shape to the comma, and added the semicolon; the comma denoting the shortest pause, the semicolon next, then the colon, and the full point terminating the sentence. The marks of interrogation and admiration were introduced many years after.’
By the 19th century, punctuation in the western world had evolved ‘to classify the marks hierarchically, in terms of weight’.
Conveying the use of Punctuation by Example
Cecil B. Hartley's teaching poem taken from his title
The Gentlemen's Book of Etiquette and Manual of Politeness,
published in 1860 identifies the relative values of punctuation marks:
The stop point out, with truth, the time of pause
A sentence doth require at ev'ry clause.
At ev'ry comma, stop while one you count;
At semicolon, two is the amount;
A colon doth require the time of three;
The period four, as learned men agree.
The use of punctuation was not standardised until after the invention of printing.According to the 1885 edition of The American Printer, the importance of punctuation was noted in various sayings by children such as:
Charles the First walked and talked
Half an hour after his head was cut off.
With a semi-colon and a comma added it reads:
Charles the First walked and talked;
Half an hour after, his head was cut off.
Andrew M McTiernan 8/November/2017

BBC - Languages - Languages - Languages of the world ...
www.bbc.co.uk/languages/guide/languages.shtml?
Languages of the world. A guide to which languages are most widely spoken, hardest to learn and other revealing facts. Open/close. 1. How many languages ...
It’s estimated that up to 7,000 different languages are spoken around the world. 90% of these languages are used by less than 100,000 people. Over a million people converse in 150-200 languages and 46 languages have just a single speaker!
Languages are grouped into families that share a common ancestry. For example, English is related to German and Dutch, and they are all part of the Indo-European family of languages. These also include Romance languages, such as French, Spanish and Italian, which come from Latin.
2,200 of the world’s languages can be found in Asia, while Europe has a mere 260.
Nearly every language uses a similar grammatical structure, even though they may not be linked in vocabulary or origin. Communities which are usually isolated from each other because of mountainous geography may have developed multiple languages. Papua New Guinea for instance, boasts no less than 832 different languages!
Exactly How Many Languages Are There in the World?
www.translationblog.co.uk/exactly-how-many-languages-are-there-in-th...?
Jan 11, 2010 – One of the challenges we face as a language solutions provider is covering demand for the languages that our clients request on a daily basis.
Richard Loyer | January 11, 2010
Exactly How Many Languages Are There in the World?
One of the challenges we face as a language solutions provider is covering demand for the languages that our clients request on a daily basis. So how many languages are there in the World and how do we go about providing translation and interpreting in all of them….?
The invaluable Ethnologue quotes 6909 living languages, that’s one language for every 862,000 people on Earth. Let’s look at some more figures from Ethnologue’s database.
Europe, with ¼ of the World’s population has only 234 languages spoken on a daily basis.
Although English does well as the World’s business language-at least for the time being- it is only 3rd in the league table of native speakers of a first language, with 328M, only 1m behind Spanish but a long way from the 845M Mandarin speakers.
94% of languages are spoken by only 6% of the World’s population, which tells us that there are hundreds of languages with just a few thousand [or hundred] speakers.
Many of these languages would be classified by some as dialects i.e. languages that have evolved from but are still quite closely related to another. This definition, of course, falls down very rapidly as most Western European languages can trace their roots to Latin but would not normally be described as dialects. Some of the African and Caribbean Patois are still seen as dialects, as was Ulster-Scots until fairly recently when it was recognised as a language. http://www.ulsterscotsagency.com/
The most famous phrase “a language is a dialect with an army and a navy” is wrongly attributed to Yiddish scholar Max Weinreich, who was probably quoting an anonymous teacher from New York, but it is a neat way to make the definition.
So how many of these languages are regularly translated by Applied Language? Well, it’s a lot but not quite 6909…….we reckon that about 200 languages are translated regularly by our global offices into documents, websites, brochures and anything else you can imagine. The range of languages required by our interpreting team is rather smaller at about 100.
The difference is no mystery; companies that translate their promotional material may be selling into every part of the globe and therefore their need is very broad whilst a hospital in Manchester, for example, will only have to deal with the resident non-native speakers and unwell tourists that come through its doors. Although the interpreting requirement is significant, it rarely exceeds 100 different languages.
Some of the most difficult requests are for languages that unfortunately don’t exist; enquiries for “Indian” or “Eastern European” do pop up occasionally. Similarly, “African” or “South American” can have us scratching our heads.
As a final thought for those of you currently learning another language you might be slightly discouraged by a report from Swarthmore College linguist K. David Harrison who predicts that 90% of the World’s languages will be extinct by 2050. http://www.msnbc.msn.com/id/438742
This might make finding translators a little easier, but would surely make our World a rather less interesting place?
Alphabet - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/Alphabet?
An alphabet is a standard set of letters (basic written symbols or graphemes) which is used to write one or more languages based on the general principle that ...
Alphabet
From Wikipedia, the free encyclopedia
This article is about sets of letters used in written languages. For other uses, see Alphabet (disambiguation).
An alphabet is a standard set of letters (basic written symbols or graphemes) which is used to write one or more languages based on the general principle that the letters represent phonemes (basic significant sounds) of the spoken language. This is in contrast to other types of writing systems, such as syllabaries (in which each character represents a syllable) and logographies (in which each character represents a word, morpheme or semantic unit).
A true alphabet has letters for the vowels of a language as well as the consonants. The first "true alphabet" in this sense is believed to be the Greek alphabet,[1][2] which is a modified form of the Phoenician alphabet. In other types of alphabet either the vowels are not indicated at all, as was the case in the Phoenician alphabet (such systems are known as abjads), or else the vowels are shown by diacritics or modification of consonants, as in the devanagari used in India and Nepal (these systems are known as abugidas or alphasyllabaries).
There are dozens of alphabets in use today, the most popular being the Latin alphabet[3] (which was derived from the Greek). Many languages use modified forms of the Latin alphabet, with additional letters formed using diacritical marks. While most alphabets have letters composed of lines (linear writing), there are also exceptions such as the alphabets used in Braille, fingerspelling, and Morse code.
Alphabets are usually associated with a standard ordering of their letters. This makes them useful for purposes of collation, specifically by allowing words to be sorted in alphabetical order. It also means that their letters can be used as an alternative method of "numbering" ordered items, in such contexts as numbered lists.
Contents
[hide] 1 Etymology
2 History 2.1 Middle Eastern scripts
2.2 European alphabets
2.3 Asian alphabets
3 Types
4 Alphabetical order
5 Names of letters
6 Orthography and pronunciation
7 See also
8 References
9 Bibliography
10 External links
Etymology[edit]
The English word alphabet came into Middle English from the Late Latin word alphabetum, which in turn originated in the Greek ??f?ß?t?? (alphabetos), from alpha and beta, the first two letters of the Greek alphabet.[4] Alpha and beta in turn came from the first two letters of the Phoenician alphabet, and originally meant ox and house respectively.
History[edit]
Main article: History of the alphabet
A Specimen of typeset fonts and languages, by William Caslon, letter founder; from the 1728 Cyclopaedia.
Middle Eastern scripts[edit]
The history of the alphabet started in ancient Egypt. By the 27th century BC Egyptian writing had a set of some 24 hieroglyphs which are called uniliterals,[5] to represent syllables that begin with a single consonant of their language, plus a vowel (or no vowel) to be supplied by the native speaker. These glyphs were used as pronunciation guides for logograms, to write grammatical inflections, and, later, to transcribe loan words and foreign names.[6]
A specimen of Proto-Sinaitic script, one of the earliest (if not the very first) phonemic scripts
In the Middle Bronze Age an apparently "alphabetic" system known as the Proto-Sinaitic script appears in Egyptian turquoise mines in the Sinai peninsula dated to circa the 15th century BC, apparently left by Canaanite workers. In 1999, John and Deborah Darnell discovered an even earlier version of this first alphabet at Wadi el-Hol dated to circa 1800 BC and showing evidence of having been adapted from specific forms of Egyptian hieroglyphs that could be dated to circa 2000 BC, strongly suggesting that the first alphabet had been developed circa that time.[7] Based on letter appearances and names, it is believed to be based on Egyptian hieroglyphs.[8] This script had no characters representing vowels. An alphabetic cuneiform script with 30 signs including three which indicate the following vowel was invented in Ugarit before the 15th century BC. This script was not used after the destruction of Ugarit.[9]
The Proto-Sinaitic script eventually developed into the Phoenician alphabet, which is conventionally called "Proto-Canaanite" before ca. 1050 BC.[10] The oldest text in Phoenician script is an inscription on the sarcophagus of King Ahiram. This script is the parent script of all western alphabets. By the tenth century two other forms can be distinguished namely Canaanite and Aramaic. The Aramaic gave rise to Hebrew.[11] The South Arabian alphabet, a sister script to the Phoenician alphabet, is the script from which the Ge'ez alphabet (an abugida) is descended. Vowelless alphabets, which are not true alphabets, are called abjads, currently exemplified in scripts including Arabic, Hebrew, and Syriac. The omission of vowels was not a satisfactory solution and some "weak" consonants were used to indicate the vowel quality of a syllable (matres lectionis). These had dual function since they were also used as pure consonants.[12]
The Proto-Sinatic or Proto Canaanite script and the Ugaritic script were the first scripts with limited number of signs, in contrast to the other widely used writing systems at the time, Cuneiform, Egyptian hieroglyphs, and Linear B. The Phoenician script was probably the first phonemic script[8][10] and it contained only about two dozen distinct letters, making it a script simple enough for common traders to learn. Another advantage of Phoenician was that it could be used to write down many different languages, since it recorded words phonemically.
The script was spread by the Phoenicians, across the Mediterranean.[10] In Greece, the script was modified to add the vowels, giving rise to the ancestor of all alphabets in the West. The indication of the vowels is the same way as the indication of the consonants, therefore it was the first true alphabet. The Greeks took letters which did not represent sounds that existed in Greek, and changed them to represent the vowels. The vowels are significant in the Greek language, and the syllabical Linear B script which was used by the Mycenaean Greeks from the 16th century BC had 87 symbols including 5 vowels. In its early years, there were many variants of the Greek alphabet, a situation which caused many different alphabets to evolve from it.
European alphabets[edit]
Codex Zographensis in the Glagolitic alphabet from Medieval Bulgaria
The Greek alphabet, in its Euboean form, was carried over by Greek colonists to the Italian peninsula, where it gave rise to a variety of alphabets used to write the Italic languages. One of these became the Latin alphabet, which was spread across Europe as the Romans expanded their empire. Even after the fall of the Roman state, the alphabet survived in intellectual and religious works. It eventually became used for the descendant languages of Latin (the Romance languages) and then for most of the other languages of Europe.
Some adaptations of the Latin alphabet are augmented with ligatures, such as æ in Old English and Icelandic and ? in Algonquian; by borrowings from other alphabets, such as the thorn þ in Old English and Icelandic, which came from the Futhark runes; and by modifying existing letters, such as the eth ð of Old English and Icelandic, which is a modified d. Other alphabets only use a subset of the Latin alphabet, such as Hawaiian, and Italian, which uses the letters j, k, x, y and w only in foreign words.
Another notable script is Elder Futhark, which is believed to have evolved out of one of the Old Italic alphabets. Elder Futhark gave rise to a variety of alphabets known collectively as the Runic alphabets. The Runic alphabets were used for Germanic languages from AD 100 to the late Middle Ages. Its usage is mostly restricted to engravings on stone and jewelry, although inscriptions have also been found on bone and wood. These alphabets have since been replaced with the Latin alphabet, except for decorative usage for which the runes remained in use until the 20th century.
The Old Hungarian script is a contemporary writing system of the Hungarians. It was in use during the entire history of Hungary, albeit not as an official writing system. From the 19th century it once again became more and more popular.
The Glagolitic alphabet was the initial script of the liturgical language Old Church Slavonic and became, together with the Greek uncial script, the basis of the Cyrillic script. Cyrillic is one of the most widely used modern alphabetic scripts, and is notable for its use in Slavic languages and also for other languages within the former Soviet Union. Cyrillic alphabets include the Serbian, Macedonian, Bulgarian, and Russian alphabets. The Glagolitic alphabet is believed to have been created by Saints Cyril and Methodius, while the Cyrillic alphabet was invented by the Bulgarian scholar Clement of Ohrid, who was their disciple. They feature many letters that appear to have been borrowed from or influenced by the Greek alphabet and the Hebrew alphabet.
Asian alphabets[edit]
Beyond the logographic Chinese writing, many phonetic scripts are in existence in Asia. The Arabic alphabet, Hebrew alphabet, Syriac alphabet, and other abjads of the Middle East are developments of the Aramaic alphabet, but because these writing systems are largely consonant-based they are often not considered true alphabets.
Most alphabetic scripts of India and Eastern Asia are descended from the Brahmi script, which is often believed to be a descendant of Aramaic.
Zhuyin on a cell phone
In Korea, the Hangul alphabet was created by Sejong the Great[13] Hangul is a unique alphabet: it is a featural alphabet, where many of the letters are designed from a sound's place of articulation (P to look like the widened mouth, L to look like the tongue pulled in, etc.); its design was planned by the government of the day; and it places individual letters in syllable clusters with equal dimensions, in the same way as Chinese characters, to allow for mixed-script writing[citation needed] (one syllable always takes up one type-space no matter how many letters get stacked into building that one sound-block).
Zhuyin (sometimes called Bopomofo) is a semi-syllabary used to phonetically transcribe Mandarin Chinese in the Republic of China. After the later establishment of the People's Republic of China and its adoption of Hanyu Pinyin, the use of Zhuyin today is limited, but it's still widely used in Taiwan where the Republic of China still governs. Zhuyin developed out of a form of Chinese shorthand based on Chinese characters in the early 1900s and has elements of both an alphabet and a syllabary. Like an alphabet the phonemes of syllable initials are represented by individual symbols, but like a syllabary the phonemes of the syllable finals are not; rather, each possible final (excluding the medial glide) is represented by its own symbol. For example, luan is represented as ??? (l-u-an), where the last symbol ? represents the entire final -an. While Zhuyin is not used as a mainstream writing system, it is still often used in ways similar to a romanization system—that is, for aiding in pronunciation and as an input method for Chinese characters on computers and cellphones.
European alphabets, especially Latin and Cyrillic, have been adapted for many languages of Asia. Arabic is also widely used, sometimes as an abjad (as with Urdu and Persian) and sometimes as a complete alphabet (as with Kurdish and Uyghur).
Types[edit]
Alphabets: Armenian , Cyrillic , Georgian , Greek , Latin , Latin (and Arabic) , Latin and Cyrillic
Abjads: Arabic , Hebrew
Abugidas: North Indic , South Indic , Ge'ez , Tana , Canadian Syllabic and Latin
Logographic+syllabic: Pure logographic , Mixed logographic and syllabaries , Featural-alphabetic syllabary + limited logographic , Featural-alphabetic syllabary
History of the alphabet[show]
--------------------------------------------------------------------------------
The term "alphabet" is used by linguists and paleographers in both a wide and a narrow sense. In the wider sense, an alphabet is a script that is segmental at the phoneme level—that is, it has separate glyphs for individual sounds and not for larger units such as syllables or words. In the narrower sense, some scholars distinguish "true" alphabets from two other types of segmental script, abjads and abugidas. These three differ from each other in the way they treat vowels: abjads have letters for consonants and leave most vowels unexpressed; abugidas are also consonant-based, but indicate vowels with diacritics to or a systematic graphic modification of the consonants. In alphabets in the narrow sense, on the other hand, consonants and vowels are written as independent letters.[14] The earliest known alphabet in the wider sense is the Wadi el-Hol script, believed to be an abjad, which through its successor Phoenician is the ancestor of modern alphabets, including Arabic, Greek, Latin (via the Old Italic alphabet), Cyrillic (via the Greek alphabet) and Hebrew (via Aramaic).
Examples of present-day abjads are the Arabic and Hebrew scripts; true alphabets include Latin, Cyrillic, and Korean hangul; and abugidas are used to write Tigrinya, Amharic, Hindi, and Thai. The Canadian Aboriginal syllabics are also an abugida rather than a syllabary as their name would imply, since each glyph stands for a consonant which is modified by rotation to represent the following vowel. (In a true syllabary, each consonant-vowel combination would be represented by a separate glyph.)
All three types may be augmented with syllabic glyphs. Ugaritic, for example, is basically an abjad, but has syllabic letters for /?a, ?i, ?u/. (These are the only time vowels are indicated.) Cyrillic is basically a true alphabet, but has syllabic letters for /ja, je, ju/ (?, ?, ?); Coptic has a letter for /ti/. Devanagari is typically an abugida augmented with dedicated letters for initial vowels, though some traditions use ? as a zero consonant as the graphic base for such vowels.
The boundaries between the three types of segmental scripts are not always clear-cut. For example, Sorani Kurdish is written in the Arabic script, which is normally an abjad. However, in Kurdish, writing the vowels is mandatory, and full letters are used, so the script is a true alphabet. Other languages may use a Semitic abjad with mandatory vowel diacritics, effectively making them abugidas. On the other hand, the Phagspa script of the Mongol Empire was based closely on the Tibetan abugida, but all vowel marks were written after the preceding consonant rather than as diacritic marks. Although short a was not written, as in the Indic abugidas, one could argue that the linear arrangement made this a true alphabet. Conversely, the vowel marks of the Tigrinya abugida and the Amharic abugida (ironically, the original source of the term "abugida") have been so completely assimilated into their consonants that the modifications are no longer systematic and have to be learned as a syllabary rather than as a segmental script. Even more extreme, the Pahlavi abjad eventually became logographic. (See below.)
Ge'ez Script of Ethiopia
Thus the primary classification of alphabets reflects how they treat vowels. For tonal languages, further classification can be based on their treatment of tone, though names do not yet exist to distinguish the various types. Some alphabets disregard tone entirely, especially when it does not carry a heavy functional load, as in Somali and many other languages of Africa and the Americas. Such scripts are to tone what abjads are to vowels. Most commonly, tones are indicated with diacritics, the way vowels are treated in abugidas. This is the case for Vietnamese (a true alphabet) and Thai (an abugida). In Thai, tone is determined primarily by the choice of consonant, with diacritics for disambiguation. In the Pollard script, an abugida, vowels are indicated by diacritics, but the placement of the diacritic relative to the consonant is modified to indicate the tone. More rarely, a script may have separate letters for tones, as is the case for Hmong and Zhuang. For most of these scripts, regardless of whether letters or diacritics are used, the most common tone is not marked, just as the most common vowel is not marked in Indic abugidas; in Zhuyin not only is one of the tones unmarked, but there is a diacritic to indicate lack of tone, like the virama of Indic.
The number of letters in an alphabet can be quite small. The Book Pahlavi script, an abjad, had only twelve letters at one point, and may have had even fewer later on. Today the Rotokas alphabet has only twelve letters. (The Hawaiian alphabet is sometimes claimed to be as small, but it actually consists of 18 letters, including the ?okina and five long vowels.) While Rotokas has a small alphabet because it has few phonemes to represent (just eleven), Book Pahlavi was small because many letters had been conflated—that is, the graphic distinctions had been lost over time, and diacritics were not developed to compensate for this as they were in Arabic, another script that lost many of its distinct letter shapes. For example, a comma-shaped letter represented g, d, y, k, or j. However, such apparent simplifications can perversely make a script more complicated. In later Pahlavi papyri, up to half of the remaining graphic distinctions of these twelve letters were lost, and the script could no longer be read as a sequence of letters at all, but instead each word had to be learned as a whole—that is, they had become logograms as in Egyptian Demotic. The alphabet in the Polish language contains 32 letters.
The largest segmental script is probably an abugida, Devanagari. When written in Devanagari, Vedic Sanskrit has an alphabet of 53 letters, including the visarga mark for final aspiration and special letters for kš and jñ, though one of the letters is theoretical and not actually used. The Hindi alphabet must represent both Sanskrit and modern vocabulary, and so has been expanded to 58 with the khutma letters (letters with a dot added) to represent sounds from Persian and English.
The largest known abjad is Sindhi, with 51 letters. The largest alphabets in the narrow sense include Kabardian and Abkhaz (for Cyrillic), with 58 and 56 letters, respectively, and Slovak (for the Latin script), with 46. However, these scripts either count di- and tri-graphs as separate letters, as Spanish did with ch and ll until recently, or uses diacritics like Slovak c. The largest true alphabet where each letter is graphically independent is probably Georgian, with 41 letters.
Syllabaries typically contain 50 to 400 glyphs, and the glyphs of logographic systems typically number from the many hundreds into the thousands. Thus a simple count of the number of distinct symbols is an important clue to the nature of an unknown script.
Alphabetical order[edit]
Main article: Alphabetical order
Alphabets often come to be associated with a standard ordering of their letters, which can then be used for purposes of collation – namely for the listing of words and other items in what is called alphabetical order.
The basic ordering of the Latin alphabet (ABCDEFGHIJKLMNOPQRSTUVWXYZ), which is derived from the Northwest Semitic "Abgad" order,[15] is well established, although languages using this alphabet have different conventions for their treatment of modified letters (such as the French é, à, and ô) and of certain combinations of letters (multigraphs). In French, these are not considered to be additional letters for the purposes of collation. However, in Icelandic, the accented letters such as á, í, and ö are considered to be distinct letters of the alphabet. In Spanish, ñ is considered a separate letter, but accented vowels such as á and é are not. The ll and ch were also considered single letters, but in 1994 the Real Academia Española changed collating order so that ll is between lk and lm in the dictionary and ch is between cg and ci, and in 2010 the tenth congress of the Association of Spanish Language Academies changed it so they were no longer letters at all[16][17]
In German, words starting with sch- (constituting the German phoneme /?/) would be intercalated between words with initial sca- and sci- (all incidentally loanwords) instead of this graphic cluster appearing after the letter s, as though it were a single letter—a lexicographical policy which would be de rigueur in a dictionary of Albanian, i.e. dh-, ë-, gj-, ll-, rr-, th-, xh- and zh- (all representing phonemes and considered separate single letters) would follow the letters d, e, g, l, n, r, t, x and z respectively. Nor is, in a dictionary of English, the lexical section with initial th- reserved a place after the letter t, but is inserted between te- and ti-. German words with umlaut would further be alphabetized as if there were no umlaut at all—contrary to Turkish which allegedly adopted the German graphemes ö and ü, and where a word like tüfek, would come after tuz, in the dictionary. An exception is the German phonebook where umlauts are sorted like ä = ae since names as Jäger appear also with the spelling Jaeger, and there's no telling them apart in the spoken language.
The Danish and Norwegian alphabets end with æ—ø—å, whereas the Icelandic, Swedish, Finnish and Estonian ones conventionally put å—ä—ö at the end.
It is unknown whether the earliest alphabets had a defined sequence. Some alphabets today, such as the Hanuno'o script, are learned one letter at a time, in no particular order, and are not used for collation where a definite order is required. However, a dozen Ugaritic tablets from the fourteenth century BC preserve the alphabet in two sequences. One, the ABCDE order later used in Phoenician, has continued with minor changes in Hebrew, Greek, Armenian, Gothic, Cyrillic, and Latin; the other, HMHLQ, was used in southern Arabia and is preserved today in Ethiopic.[18] Both orders have therefore been stable for at least 3000 years.
The historical order was abandoned in Runic and Arabic, although Arabic retains the traditional abjadi order for numbering.
The Brahmic family of alphabets used in India use a unique order based on phonology: The letters are arranged according to how and where they are produced in the mouth. This organization is used in Southeast Asia, Tibet, Korean hangul, and even Japanese kana, which is not an alphabet.
Names of letters[edit]
The Phoenician letter names, in which each letter was associated with a word that begins with that sound, continue to be used to varying degrees in Samaritan, Aramaic, Syriac, Hebrew, Greek and Arabic. The names were abandoned in Latin, which instead referred to the letters by adding a vowel (usually e) before or after the consonant (the exception is zeta, which was retained from Greek). In Cyrillic originally the letters were given names based on Slavic words; this was later abandoned as well in favor of a system similar to that used in Latin.
Orthography and pronunciation[edit]
Main article: Phonemic orthography
When an alphabet is adopted or developed for use in representing a given language, an orthography generally comes into being, providing rules for the spelling of words in that language. In accordance with the principle on which alphabets are based, these rules will generally map letters of the alphabet to the phonemes (significant sounds) of the spoken language. In a perfectly phonemic orthography there would be a consistent one-to-one correspondence between the letters and the phonemes, so that a writer could predict the spelling of a word given its pronunciation, and a speaker could predict the pronunciation of a word given its spelling. However this ideal is not normally achieved in practice; some languages (such as Spanish and Finnish) come close to it, while others (such as English) deviate from it to a much larger degree.
The pronunciation of a language often evolves independently of its writing system, and writing systems have been borrowed for languages they were not designed for, so the degree to which letters of an alphabet correspond to phonemes of a language varies greatly from one language to another and even within a single language.
Languages may fail to achieve a one-to-one correspondence between letters and sounds in any of several ways:
A language may represent a given phoneme with a combination of letters rather than just a single letter. Two-letter combinations are called digraphs and three-letter groups are called trigraphs. German uses the tesseragraphs (four letters) "tsch" for the phoneme [t?] and "dsch" for [d?], although the latter is rare. Kabardian also uses a tesseragraph for one of its phonemes, namely "????". Two letters representing one sound is widely used in Hungarian as well (where, for instance, cs stands for [c], sz for [s], zs for [ž], dzs for [j], etc.).
A language may represent the same phoneme with two different letters or combinations of letters. An example is modern Greek which may write the phoneme [i] in six different ways: ???, ???, ???, ?e??, ????, and ???? (although the last is rare).
A language may spell some words with unpronounced letters that exist for historical or other reasons. For example, the spelling of the Thai word for "beer" [??????] retains a letter for the final consonant "r" present in the English word it was borrowed from, but silences it.
Pronunciation of individual words may change according to the presence of surrounding words in a sentence (sandhi).
Different dialects of a language may use different phonemes for the same word.
A language may use different sets of symbols or different rules for distinct sets of vocabulary items, such as the Japanese hiragana and katakana syllabaries, or the various rules in English for spelling words from Latin and Greek, or the original Germanic vocabulary.
National languages generally elect to address the problem of dialects by simply associating the alphabet with the national standard. However, with an international language with wide variations in its dialects, such as English, it would be impossible to represent the language in all its variations with a single phonetic alphabet.
Some national languages like Finnish, Turkish, Serbo-Croatian (Serbian, Croatian and Bosnian) and Bulgarian have a very regular spelling system with a nearly one-to-one correspondence between letters and phonemes. Strictly speaking, these national languages lack a word corresponding to the verb "to spell" (meaning to split a word into its letters), the closest match being a verb meaning to split a word into its syllables. Similarly, the Italian verb corresponding to 'spell (out)', compitare, is unknown to many Italians because the act of spelling itself is rarely needed: Italian spelling is highly phonemic. In standard Spanish, it is possible to tell the pronunciation of a word from its spelling, but not vice versa; this is because certain phonemes can be represented in more than one way, but a given letter is consistently pronounced. French, with its silent letters and its heavy use of nasal vowels and elision, may seem to lack much correspondence between spelling and pronunciation, but its rules on pronunciation, though complex, are actually consistent and predictable with a fair degree of accuracy.
At the other extreme are languages such as English, where the spelling of many words simply has to be memorized as they do not correspond to sounds in a consistent way. For English, this is partly because the Great Vowel Shift occurred after the orthography was established, and because English has acquired a large number of loanwords at different times, retaining their original spelling at varying levels. Even English has general, albeit complex, rules that predict pronunciation from spelling, and these rules are successful most of the time; rules to predict spelling from the pronunciation have a higher failure rate.
Sometimes, countries have the written language undergo a spelling reform to realign the writing with the contemporary spoken language. These can range from simple spelling changes and word forms to switching the entire writing system itself, as when Turkey switched from the Arabic alphabet to a Turkish alphabet of Latin origin.
The sounds of speech of all languages of the world can be written by a rather-small universal phonetic-alphabet. A standard for this is the International Phonetic Alphabet.
See also[edit]
A Is For Aardvark
Abecedarium
Acrophony
Akshara
Alphabet Effect
Alphabet song
Alphabetical order
Alphabetize
Butterfly Alphabet
Character encoding
Constructed script
Cyrillic
English alphabet
Hangul
ICAO spelling alphabet
Lipogram
List of alphabets
Pangram
Thai script
Transliteration
Unicode
References[edit]
1.^ Coulmas, Florian (1996). The Blackwell Encyclopedia of Writing Systems. Oxford: Blackwell Publishing. ISBN 0-631-21481-X.
2.^ Millard 1986, p. 396
3.^ Haarmann 2004, p. 96
4.^ Encyclopædia Britannica Online – Merriam-Webster's Online Dictionary
5.^ "The Development of the Western Alphabet". h2g2. BBC. 2004-04-08. Retrieved 2008-08-04.
6.^ Daniels and Bright (1996), pp. 74–75
7.^ J. C. Darnell, F. W. Dobbs-Allsopp, Marilyn J. Lundberg, P. Kyle McCarter, and Bruce Zuckermanet, “Two early alphabetic inscriptions from the Wadi el-Hol: new evidence for the origin of the alphabet from the western desert of Egypt.” The Annual of the American Schools of Oriental Research, 59 (2005).
8.^ a b Coulmas (1989), p. 140–141.
9.^ Ugaritic Writing online
10.^ a b c Daniels and Bright (1996), pp 92-96
11.^ "Coulmas"(1989),p.142
12.^ "Coulmas" (1989) p.147.
13.^ "?????????…??????(His majesty created 28 characters himself... It is Hunminjeongeum (original name for Hangul))", «???? (The Annals of the Choson Dynasty : Sejong)» 25? 12?.
14.^ For critics of the abjad-abugida-alphabet distinction, see Reinhard G. Lehmann: "27-30-22-26. How Many Letters Needs an Alphabet? The Case of Semitic", in: The idea of writing: Writing across borders / edited by Alex de Voogt and Joachim Friedrich Quack, Leiden: Brill 2012, p. 11-52, esp p. 22-27
15.^ Reinhard G. Lehmann: "27-30-22-26. How Many Letters Needs an Alphabet? The Case of Semitic", in: The idea of writing: Writing across borders / edited by Alex de Voogt and Joachim Friedrich Quack, Leiden: Brill 2012, p. 11-52
16.^ Real Academia Española. "Spanish Pronto!: Spanish Alphabet." Spanish Pronto! 22 April 2007. January 2009 Spanish Pronto: Spanish < > English Medical Translators.
17.^ "La “i griega” se llamará “ye”". Cuba Debate. 2010-11-05. Retrieved 12 December 2010. Cubadebate.cu
18.^ Millard, A.R. "The Infancy of the Alphabet", World Archaeology 17, No. 3, Early Writing Systems (February 1986): 390–398. page 395.
Bibliography[edit]
Coulmas, Florian (1989). The Writing Systems of the World. Blackwell Publishers Ltd. ISBN 0-631-18028-1.
Daniels, Peter T.; Bright, William (1996). The World's Writing Systems. Oxford University Press. ISBN 0-19-507993-0. Overview of modern and some ancient writing systems.
Driver, G. R. (1976). Semitic Writing (Schweich Lectures on Biblical Archaeology S.) 3Rev Ed. Oxford University Press. ISBN 0-19-725917-0.
Haarmann, Harald (2004). Geschichte der Schrift (2nd ed.). München: C. H. Beck. ISBN 3-406-47998-7
Hoffman, Joel M. (2004). In the Beginning: A Short History of the Hebrew Language. NYU Press. ISBN 0-8147-3654-8. Chapter 3 traces and summarizes the invention of alphabetic writing.
Logan, Robert K. (2004). The Alphabet Effect: A Media Ecology Understanding of the Making of Western Civilization. Hampton Press. ISBN 1-57273-523-6.
McLuhan, Marshall; Logan, Robert K. (1977). Alphabet, Mother of Invention. Etcetera. Vol. 34, pp. 373–383
Millard, A. R. (1986). "The Infancy of the Alphabet". World Archaeology 17 (3): 390–398. doi:10.1080/00438243.1986.9979978
Ouaknin, Marc-Alain; Bacon, Josephine (1999). Mysteries of the Alphabet: The Origins of Writing. Abbeville Press. ISBN 0-7892-0521-1.
Powell, Barry (1991). Homer and the Origin of the Greek Alphabet. Cambridge University Press. ISBN 0-521-58907-X.
Powell, Barry B. 2009. Writing: Theory and History of the Technology of Civilization, Oxford: Blackwell. ISBN 978-1-4051-6256-2
Sacks, David (2004). Letter Perfect: The Marvelous History of Our Alphabet from A to Z (PDF). Broadway Books. ISBN 0-7679-1173-3.
Saggs, H. W. F. (1991). Civilization Before Greece and Rome. Yale University Press. ISBN 0-300-05031-3. Chapter 4 traces the invention of writing
External links[edit]
Look up alphabet in Wiktionary, the free dictionary.
The Origins of abc
"Language, Writing and Alphabet: An Interview with Christophe Rico", Damqatum 3 (2007)
Alphabetic Writing Systems
Michael Everson's Alphabets of Europe
Evolution of alphabets, animation by Prof. Robert Fradkin at the University of Maryland
How the Alphabet Was Born from Hieroglyphs—Biblical Archaeology Review
English alphabet - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/English_alphabet?
The modern English alphabet is a Latin alphabet consisting of 26 letters – the same letters that are found in the ISO basic Latin alphabet:...
English alphabet
From Wikipedia, the free encyclopedia
"The Alphabet" redirects here. For the short film by David Lynch, see The Alphabet (film).
The modern English alphabet is a Latin alphabet consisting of 26 letters – the same letters that are found in the ISO basic Latin alphabet:
Majuscule forms (also called uppercase or capital letters)
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Minuscule forms (also called lowercase or small letters)
a b c d e f g h i j k l m n o p q r s t u v w x y z
The exact shape of printed letters varies depending on the typeface. The shape of handwritten letters can differ significantly from the standard printed form (and between individuals), especially when written in cursive style. See the individual letter articles for information about letter shapes and origins (follow the links on any of the uppercase letters above).
Written English uses a number of digraphs, such as ch, sh, th, wh, qu, etc., but they are not considered separate letters of the alphabet. Some traditions also use two ligatures, æ and œ,[1] or consider the ampersand (&) part of the alphabet.
English alphabet
Contents
[hide] 1 History 1.1 Old English
1.2 Modern English
2 Diacritics
3 Ampersand
4 Apostrophe
5 Letter names 5.1 Etymology
6 Phonology
7 Letter frequencies
8 See also
9 Footnotes
History[edit]
See also: History of the Latin alphabet and English orthography
Old English[edit]
Main article: Old English Latin alphabet
The English language was first written in the Anglo-Saxon futhorc runic alphabet, in use from the 5th century. This alphabet was brought to what is now England, along with the proto-form of the language itself, by Anglo-Saxon settlers. Very few examples of this form of written Old English have survived, these being mostly short inscriptions or fragments.
The Latin script, introduced by Christian missionaries, began to replace the Anglo-Saxon futhorc from about the 7th century, although the two continued in parallel for some time. Futhorc influenced the emerging English alphabet by providing it with the letters thorn (Þ þ) and wynn (? ?). The letter eth (Ð ð) was later devised as a modification of dee (D d), and finally yogh (? ?) was created by Norman scribes from the insular g in Old English and Irish, and used alongside their Carolingian g.
The a-e ligature ash (Æ æ) was adopted as a letter its own right, named after a futhorc rune æsc. In very early Old English the o-e ligature ethel (Œ œ) also appeared as a distinct letter, likewise named after a rune, œðel. Additionally, the v-v or u-u ligature double-u (W w) was in use.
In the year 1011, a writer named Byrhtferð ordered the Old English alphabet for numerological purposes.[2] He listed the 24 letters of the Latin alphabet (including ampersand) first, then 5 additional English letters, starting with the Tironian note ond (?) an insular symbol for and:
A B C D E F G H I K L M N O P Q R S T V X Y Z & ? ? Þ Ð Æ
Modern English[edit]
In the orthography of Modern English, thorn (þ), eth (ð), wynn (?), yogh (?), ash (æ), and ethel (œ) are obsolete. Latin borrowings reintroduced homographs of ash and ethel into Middle English and Early Modern English, though they are not considered to be the same letters[citation needed] but rather ligatures, and in any case are somewhat old-fashioned. Thorn and eth were both replaced by th,[citation needed] though thorn continued in existence for some time, its lowercase form gradually becoming graphically indistinguishable from the minuscule y in most handwriting. Y for th can still be seen in pseudo-archaisms such as "Ye Olde Booke Shoppe". The letters þ and ð are still used in present-day Icelandic and Faroese. Wynn disappeared from English around the fourteenth century when it was supplanted by uu, which ultimately developed into the modern w. Yogh disappeared around the fifteenth century and was typically replaced by gh.
The letters u and j, as distinct from v and i, were introduced in the 16th century, and w assumed the status of an independent letter, so that the English alphabet is now considered to consist of the following 26 letters:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
The variant lowercase form long s (?) lasted into early modern English, and was used in non-final position up to the early 19th century.
The ligatures æ and œ are still used in formal writing for certain words of Greek or Latin origin, such as encyclopædia and cœlom. Lack of awareness and technological limitations (such as their absence from the standard qwerty keyboard) have made it common to see these rendered as "ae" and "oe", respectively, in modern, non-academic usage. These ligatures are not used in American English, where a lone e has mostly supplanted both (for example, encyclopedia for encyclopædia, and fetus for fœtus).
Diacritics[edit]
Main article: English terms with diacritical marks
Question book-new.svg
This section does not cite any references or sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2011)
Diacritic marks mainly appear in loanwords such as naïve and façade. As such words become naturalised In English, there is a tendency to drop the diacritics, as has happened with old borrowings such as hôtel, from French. Informal English writing tends to omit diacritics because of their absence from the computer keyboard, while professional copywriters and typesetters tend to include them. Words that are still perceived as foreign tend to retain them; for example, the only spelling of soupçon found in English dictionaries (the OED and others) uses the diacritic. Diacritics are also more likely to be retained where there would otherwise be confusion with another word (for example, résumé rather than resume), and, rarely, even added (as in maté, from Spanish yerba mate, but following the pattern of café, from French).
Occasionally, especially in older writing, diacritics are used to indicate the syllables of a word: cursed (verb) is pronounced with one syllable, while cursèd (adjective) is pronounced with two. È is used widely in poetry, e.g. in Shakespeare's sonnets. Similarly, while in chicken coop the letters -oo- represent a single vowel sound (a digraph), in zoölogist and coöperation, they represent two. An acute, grave or diaeresis may also be placed over an 'e' at the end of a word to indicate that it is not silent, as in saké. However, in practice these devices are often not used even where they would serve to alleviate some degree of confusion.
Ampersand[edit]
The & has sometimes appeared at the end of the English alphabet, as in Byrhtferð's list of letters in 1011.[2] Historically, the figure is a ligature for the letters Et. In English it is used to represent the word and and occasionally the Latin word et, as in the abbreviation &c (et cetera).
Apostrophe[edit]
Question book-new.svg
This section does not cite any references or sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2011)
The apostrophe, while not considered part of the English alphabet, is used to abbreviate English words. A few pairs of words, such as its (belonging to it) and it's (it is or it has), were (plural of was) and we're (we are), and shed (to get rid of) and she'd (she would or she had) are distinguished in writing only by the presence or absence of an apostrophe. The apostrophe also distinguishes the possessive endings -'s and -s' from the common plural ending -s, a practice introduced in the 18th century; before, all three endings were written -s, which could lead to confusion (as in, the Apostles words).
Letter names[edit]
The names of the letters are rarely spelled out, except when used in derivations or compound words (for example tee-shirt, deejay, emcee, okay, aitchless, wye-level, etc.), derived forms (for example exed out, effing, to eff and blind, etc.), and in the names of objects named after letters (for example em (space) in printing and wye (junction) in railroading). The forms listed below are from the Oxford English Dictionary. Vowels stand for themselves, and consonants usually have the form consonant + ee or e + consonant (e.g. bee and ef). The exceptions are the letters aitch, jay, kay, cue, ar, ess (but es- in compounds ), wye, and zed. Plurals of consonants end in -s (bees, efs, ems) or, in the cases of aitch, ess, and ex, in -es (aitches, esses, exes). Plurals of vowels end in -es (aes, ees, ies, oes, ues); these are rare. Of course, all letters may stand for themselves, generally in capitalized form (okay or OK, emcee or MC), and plurals may be based on these (aes or A's, cees or C's, etc.)
Letter
Letter name
Pronunciation
A a /e?/[3]
B bee /bi?/
C cee /si?/
D dee /di?/
E e /i?/
F ef (eff as a verb) /?f/
G gee /d?i?/
H aitch /e?t?/
haitch[4] /he?t?/
I i /a?/
J jay /d?e?/
jy[5] /d?a?/
K kay /ke?/
L el or ell /?l/
M em /?m/
N en /?n/
O o /o?/
P pee /pi?/
Q cue /kju?/
R ar /?r/[6]
S ess (es-)[7] /?s/
T tee /ti?/
U u /ju?/
V vee /vi?/
W double-u /'d?b?l.ju?/[8]
X ex /?ks/
Y wy or wye /wa?/
Z zed[9] /z?d/
zee[10] /zi?/
izzard[11] /'?z?rd/
Some groups of letters, such as pee and bee, or em and en, are easily confused in speech, especially when heard over the telephone or a radio communications link. Spelling alphabets such as the ICAO spelling alphabet, used by aircraft pilots, police and others, are designed to eliminate this potential confusion by giving each letter a name that sounds quite different from any other.
Etymology[edit]
The names of the letters are for the most part direct descendents, via French, of the Latin (and Etruscan) names. (See Latin alphabet: Origins.)
Letter
Latin
Old French
Middle English
Modern English
A á /a?/ /a?/ /a?/ /e?/
B bé /be?/ /be?/ /be?/ /bi?/
C cé /ke?/ /t?e?/ ? /tse?/ ? /se?/ /se?/ /si?/
D dé /de?/ /de?/ /de?/ /di?/
E é /e?/ /e?/ /e?/ /i?/
F ef /?f/ /?f/ /?f/ /?f/
G gé /ge?/ /d?e?/ /d?e?/ /d?i?/
H há /ha?/ ? /aha/ ? /ak?a/ /a?t?/ /a?t?/ /e?t?/
I í /i?/ /i?/ /i?/ /a?/
J – – – /d?e?/
K ká /ka?/ /ka?/ /ka?/ /ke?/
L el /?l/ /?l/ /?l/ /?l/
M em /?m/ /?m/ /?m/ /?m/
N en /?n/ /?n/ /?n/ /?n/
O ó /o?/ /o?/ /o?/ /o?/
P pé /pe?/ /pe?/ /pe?/ /pi?/
Q qú /ku?/ /ky?/ /kiw/ /kju?/
R er /?r/ /?r/ / ?r/ ? /ar/ /?r/
S es /?s/ /?s/ /?s/ /?s/
T té /te?/ /te?/ /te?/ /ti?/
U ú /u?/ /y?/ /iw/ /ju?/
V – – – /vi?/
W – – – /'d?b?l.ju?/
X ex /?ks, iks/ /iks/ /?ks/ /?ks/
Y hý /hy?, i?/
í graeca /'gra?ka/ ui, gui ?
i grec /i? gr??k/ /wi?/ ? /wa?/
Z zéta /ze?ta/ zed /z??d/
et zed /et ze?d/ ? /e zed/ /z?d/
/?'z?d/ /z?d, zi?/
/'?z?d/
The regular phonological developments (in rough chronological order) are:
palatalization before front vowels of Latin /k/ successively to /t?/, /ts/, and finally to Middle French /s/. Affects C.
palatalization before front vowels of Latin /g/ to Proto-Romance and Middle French /d?/. Affects G.
fronting of Latin /u?/ to Middle French /y?/, becoming Middle English /iw/ and then Modern English /ju?/. Affects Q, U.
the inconsistent lowering of Middle English /?r/ to /ar/. Affects R.
the Great Vowel Shift, shifting all Middle English long vowels. Affects A, B, C, D, E, G, H, I, K, O, P, T, and presumably Y.
The novel forms are aitch, a regular development of Medieval Latin acca; jay, a new letter presumably vocalized like neighboring kay to avoid confusion with established gee (the other name, jy, was taken from French); vee, a new letter named by analogy with the majority; double-u, a new letter, self-explanatory (the name of Latin V was u); wye, of obscure origin but with an antecedent in Old French wi; zee, an American leveling of zed by analogy with the majority; and izzard, from the Romance phrase i zed or i zeto "and Z" said when reciting the alphabet.
Phonology[edit]
Main article: English phonology
The letters A, E, I, O, and U are considered vowel letters, since (except when silent) they represent vowels; the remaining letters are considered consonant letters, since when not silent they generally represent consonants. However, Y commonly represents vowels as well as a consonant (e.g., "myth"), as very rarely does W (e.g., "cwm"). Conversely, U sometimes represents a consonant (e.g., "quiz").
Letter frequencies[edit]
Main article: Letter frequency
The letter most frequently used in English is E. The least frequently used letter is Z.
The list below shows the frequency of letter use in English.[12]
Letter
Frequency
A 8.17%
B 1.49%
C 2.78%
D 4.25%
E 12.70%
F 2.23%
G 2.02%
H 6.09%
I 6.97%
J 0.15%
K 0.77%
L 4.03%
M 2.41%
N 6.75%
O 7.51%
P 1.93%
Q 0.10%
R 5.99%
S 6.33%
T 9.06%
U 2.76%
V 0.98%
W 2.36%
X 0.15%
Y 1.97%
Z 0.07%
See also[edit]
English orthography
English spelling reform
American manual alphabet
Two-handed manual alphabets
English braille
American braille
New York Point
Footnotes[edit]
1.^ See also the section on Ligatures
2.^ a b Michael Everson, Evertype, Baldur Sigurðsson, Íslensk Málstöð, On the Status of the Latin Letter Þorn and of its Sorting Order
3.^ Sometimes /æ/ in Hiberno-English
4.^ sometimes in Australian and Irish English, and usually in Indian English (although often considered incorrect)
5.^ in Scottish English
6.^ /?r/ (/??r/?) in Hiberno-English[citation needed]
7.^ in compounds such as es-hook
8.^ Especially in American English, the /l/ is not often pronounced in informal speech. (Merriam Webster's Collegiate Dictionary, 10th ed). Common colloquial pronunciations are /'d?b?ju?/, /'d?b?j?/, and /'d?bj?/, as in the nickname "Dubya", especially in terms like www.
9.^ in British and Commonwealth English
10.^ in American English
11.^ in Scottish English
12.^ Beker, Henry; Piper, Fred (1982). Cipher Systems: The Protection of Communications. Wiley-Interscience. p. 397. Table also available from Lewand, Robert (2000). Cryptological Mathematics. The Mathematical Association of America. p. 36. ISBN 978-0883857199. and [1]
Description of the English language
Grammar·
Phonology·
Stress and reduced vowels·
Orthography·
Alphabet·
Dialects·
Language history·
Phonological history
Categories: English spelling
Latin alphabets
Languages
???????
?????????
Cesky
Deutsch
Eesti
Español
?????
Français
Gaelg
???
??????
Magyar
??????????
Polski
Português
Româna
???????
?????
??????
Türkçe
??????????
??
Edit links
This page was last modified on 5 June 2013 at 05:21.
1234 5 6789
Letter frequency - Wikipedia, the free encyclopedia
"The most common letter in the English alphabet is E."
Daily Mail, Wednesday, December 10, 2014
ANSWERS TO CORRESPONDENTS
Compiled by Charles Legge
QUESTION A Iipogram Is a constrained form of writing where a specific letter (often a vowel) is avoided altogether. Have any novels been written this way?
THE lipogram (Greek for 'leaving out a letter') is an ancient literary form, dating back to the 6th-century BC writer Lasus of Hermione, who wrote two composition for the voice in which he suppressed the sigma, one of the most common letters in Greek.
The first person to tackle it in novel form was U.S. author Ernest Vincent Wright, Gadsby, published in 1939, has 50,000 words and is completely without the letter E. The hero of the novel is a man named John Gadsby. The author went so far as to make the E on his typewriter inoperable, to avoid an E slipping into the text inadvertently.
Naturally he had to avoid the word pronouns such as 'he', 'she', 'her', 'them' `they', and past tenses that end in '-ed'. The numbers from seven to 30 had to be omitted as, to keep the text 'pure' the author would not substitute the numerical values — quite an achievement. It took about nine years to complete then some time to find a publisher.
A poetic lipogram, probably unintentional, is the six-line nursery rhyme Old Mother Hubbard which, surprisingly, does not contain the letter i.
Going further, there is one three-stanza poem, called Fate Of Nassan, in which each four-line stanza contains every letter of the alphabet except 'e'. The poem is anonymous but was composed before 1870.
C. D. Allan, Alsager, Stoke-on-Trent, Staffs.
PERHAPS the most-famous example is the Polish-Jewish-French writer Georges Perec, who died in 1982.
His 1969 novel, La Disparition, translated. into English (1994) by Gilbert Adair as A Void, was written without a single letter `e'. Ironic, really, since his own name contains no fewer than four example of that letter.
Frederick Robinson, Bexhill-on-Sea, East Sussex
Old Mother Hubbard - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/Old_Mother_Hubbard
Old Mother Hubbard Went to the cupboard, To give the poor dog a bone; When she came there, The cupboard was bare, And so the poor dog had none.
Letter frequency - Wikipedia, the free encyclopedia
"The most common letter in the English alphabet is E."
LOOK AT THE 5FIVES LOOK AT THE 5FIVES LOOK AT THE 5FIVES THE 5FIVES THE 5FIVES
LOOK AT THE 5 LOOK AT THE 5 LOOK AT THE 5 THE 5 THE 5
Letter Frequencies in the English Language
https://www3.nd.edu › handouts › cryptography › letter...
THE INDEPENDENT MAGAZINE
Wednesday 11 September 2013
Mysteries of the snowflake: The curious world of the ice-crystal experts.
Inevitably, though, the most common question is, how can Libbrecht be so sure no two snowflakes are ever identical? He likes to tell people that physics has a Zen-like answer, “which is that it depends largely on what you mean by the question. The short answer is that if you consider there’s over a trillion ways you could arrange 15 different books on your bookshelf, then the number of ways of making a complex snowflake is so staggeringly large that, over the history of our planet, I’m confident no two identical flakes have ever fallen. The long answer is more involved – depending on what you mean by ‘alike’ and ‘snowflake’. There could be some extremely small, simple-shaped crystals that looked so alike under a microscope as to be indistinguishable – and if you sifted through enough Arctic snow, where these simple crystals are common, you could probably find a few twins.”
"The short answer is that if you consider there’s over a trillion ways you could arrange 15 different books on your bookshelf,"
SORT OUT THE WHEAT FROM THE CHAFF
Letter Frequencies in the English Language
https://www3.nd.edu › handouts › cryptography › letter...
Why is the Letter E the Most Common Letter in the English ...
https://englishlanguagethoughts.com › 2018/04/08 › w...
8 Apr 2018 — The letter makes up 12.702% of the letters in an average text, and is the most commonly-used letter in English. The next most frequently-used ...This is a question I’ve been asking myself ruefully these last few days. The E on my keyboard hasn’t been very coöperative, insisting that I bang it at least a few times for it to make the letter E appear on the screen. This has made me really… appreciate, for wont of a better word, just how often we have to use the letter E.
10 |
CODE DE CODE |
67 |
13 |
4 |
|
C+O |
18 |
9 |
|
|
D+E |
9 |
9 |
|
|
D+E |
9 |
9 |
|
|
C+O |
18 |
9 |
|
|
D+E |
9 |
9 |
|
10 |
CODE DE CODE |
63 |
36 |
36 |
1+0 |
- |
6+3 |
3+6 |
3+6 |
1 |
CODE DE CODE |
9 |
9 |
9 |
1 |
I |
9 |
9 |
9 |
3 |
SAY |
45 |
9 |
9 |
7 |
DECODER |
54 |
36 |
9 |
6 |
DECODE |
36 |
27 |
9 |
4 |
CODE |
27 |
18 |
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5 |
CODED |
31 |
22 |
4 |
5 |
CODES |
46 |
19 |
1 |
- |
CODE |
|
|
- |
2 |
C+O |
18 |
9 |
9 |
2 |
D+E |
9 |
9 |
9 |
- |
DECODE |
|
|
- |
2 |
D+E |
9 |
9 |
9 |
2 |
C+O |
18 |
9 |
9 |
2 |
D+E |
9 |
9 |
9 |
- |
DECODER |
|
|
- |
2 |
D+E |
9 |
9 |
9 |
2 |
C+O |
18 |
9 |
9 |
2 |
D+E |
9 |
9 |
9 |
1 |
R |
18 |
9 |
9 |
CODE DE CODE
C+O D+E D+E C+O D+E
9+9+9+9+9
C+O D+E D+E C+O D+E
CODE DE CODE
CODE BREAKER
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
4 |
|
27 |
18 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
60 |
33 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
87 |
51 |
51 |
5 |
|
|
|
|
|
|
|
|
|
|
|
5+1 |
|
1+1 |
|
8+7 |
5+1 |
5+1 |
|
|
|
|
|
1+5 |
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CODE BREAKER
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
87 |
51 |
51 |
5 |
|
|
|
|
|
|
|
|
|
|
|
5+1 |
|
1+1 |
|
8+7 |
5+1 |
5+1 |
|
|
|
|
|
1+5 |
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
87 |
51 |
51 |
5 |
|
|
|
|
|
|
|
|
|
|
|
5+1 |
|
1+1 |
|
8+7 |
5+1 |
5+1 |
|
|
|
|
|
1+5 |
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
87 |
51 |
51 |
5 |
|
|
|
|
|
|
|
|
|
5+1 |
|
1+1 |
|
8+7 |
5+1 |
5+1 |
|
|
|
|
|
1+5 |
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
4 |
SIGN |
49 |
22 |
4 |
S |
= |
1 |
- |
5 |
SIGNS |
68 |
23 |
5 |
S |
= |
1 |
- |
6 |
SIGNAL |
62 |
26 |
8 |
S |
= |
1 |
- |
7 |
SIGNALS |
81 |
27 |
9 |
S |
= |
1 |
- |
6 |
SIGNALLED |
164 |
38 |
2 |
S |
= |
1 |
- |
7 |
SIGNALLING |
104 |
50 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
6 |
SYMBOL |
86 |
23 |
5 |
S |
= |
1 |
- |
7 |
SYMBOLS |
105 |
24 |
6 |
S |
= |
1 |
- |
9 |
SYMBOLISE |
119 |
38 |
2 |
S |
= |
1 |
- |
9 |
SYMBOLOGY |
133 |
43 |
7 |
S |
= |
1 |
- |
10 |
SYMBOLISED |
123 |
42 |
6 |
S |
= |
1 |
- |
11 |
SYMBOLISING |
144 |
54 |
9 |
S |
= |
1 |
- |
12 |
SYMBOLOGICAL |
133 |
52 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
= |
5 |
- |
6 |
NUMBER |
73 |
28 |
1 |
N |
= |
5 |
- |
7 |
NUMBERS |
92 |
29 |
2 |
N |
= |
5 |
- |
7 |
NUMERAL |
84 |
30 |
3 |
N |
= |
5 |
- |
8 |
NUMERALS |
103 |
31 |
4 |
N |
= |
5 |
- |
9 |
NUMERICAL |
96 |
42 |
6 |
N |
= |
5 |
- |
8 |
NUMBERED |
82 |
37 |
1 |
N |
= |
5 |
- |
9 |
NUMBERING |
103 |
49 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
= |
4 |
- |
5 |
DIGIT |
49 |
31 |
4 |
D |
= |
4 |
- |
6 |
DIGITS |
68 |
32 |
5 |
D |
= |
4 |
- |
7 |
DIGITAL |
62 |
35 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
= |
3 |
- |
6 |
LETTER |
80 |
26 |
8 |
L |
= |
3 |
- |
7 |
LETTERS |
99 |
27 |
9 |
L |
= |
3 |
- |
8 |
LETTERED |
89 |
35 |
9 |
L |
= |
3 |
- |
9 |
LETTERING |
110 |
56 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
= |
3 |
- |
5 |
COUNT |
73 |
19 |
1 |
C |
= |
3 |
- |
6 |
COUNTS |
92 |
20 |
2 |
C |
= |
3 |
- |
7 |
COUNTED |
82 |
28 |
1 |
C |
= |
3 |
- |
8 |
COUNTING |
103 |
40 |
4 |
C |
= |
3 |
- |
9 |
COUNTLESS |
128 |
29 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
= |
3 |
- |
6 |
CYPHER |
75 |
39 |
3 |
C |
= |
3 |
- |
7 |
CYPHERS |
94 |
40 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
= |
5 |
- |
7 |
ENCRYPT |
101 |
38 |
2 |
E |
= |
5 |
- |
8 |
ENCRYPTS |
120 |
39 |
3 |
E |
= |
5 |
- |
9 |
ENCRYPTED |
110 |
47 |
2 |
E |
= |
5 |
- |
10 |
ENCRYPTION |
139 |
58 |
4 |
E |
= |
5 |
- |
10 |
ENCRYPTING |
131 |
59 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
4 |
GODS |
45 |
18 |
9 |
C |
= |
3 |
- |
5 |
CYCLE |
48 |
21 |
3 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
C |
= |
3 |
- |
6 |
CIRCLE |
68 |
32 |
5 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
C |
= |
3 |
- |
6 |
CIRCLE |
68 |
32 |
5 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
C |
= |
3 |
- |
5 |
CYCLE |
48 |
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
= |
3 |
- |
8 |
CREATORS |
99 |
36 |
9 |
D |
= |
4 |
- |
6 |
DIVINE |
63 |
36 |
9 |
E |
= |
5 |
- |
7 |
ETERNAL |
75 |
30 |
3 |
L |
= |
3 |
- |
6 |
LIVING |
73 |
37 |
1 |
M |
= |
4 |
- |
4 |
MIND |
40 |
22 |
4 |
Daily Mail
Thursday, June 11 2009
Page 37
Web 2.0 - the one millionth English word
ALMOST 1,500 years after it was first recorded, the English language has its one millionth word.
At 10.22am yesterday Web 2.0 - describing the next generation of internet services entered the dictionary.
To be accepted a word must be used at least 25,000 times across national boundaries and outside specialisms.
U.S-based Global Language Monitor surveys print publications, online news sites, blogs and social media for useage.
Jai Ho!, a Hindi phrase signifying the joy of victory became the 999,999th word thanks to the Oscar-Winning film Slumdog millionaire.
At 1,000,001 is Financial Tsunami - a sudden financial restructuring.
"JAI HO! A HINDI PHRASE SIGNIFYING THE JOY OF VICTORY BECAME THE 999,999TH WORD..."
THE JESUS MYSTERIES
Timothy Freke & Peter Gandy
1
999
Page 177
The gospels are actually anonymous works, in which everything, without exception, is written in capital letters, with no headings, chapter or verse divisions, and practically no punctuation or spaces between words.61 They were not even written in the Aramic of the Jews but in Greek.62
THE GOSPELS ARE ACTUALLY ANONYMOUS WORKS,
IN WHICH EVERYTHING WITHOUT EXCEPTION, IS WRITTEN IN CAPITAL LETTERS,
WITH NO PUNCTUATION OR SPACES BETWEEN WORDS.
Essenes - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Essenes
The Essenes (in Modern but not in Ancient Hebrew: אִסִּיִים, Isiyim; Greek: Εσσήνοι, Εσσαίοι, or Οσσαίοι, Essḗnoi, Essaíoi, Ossaíoi) were a sect of Second ...
Essenes
From Wikipedia, the free encyclopedia
Essene" redirects here. For the bread, see sprouted bread.
Part of a series on Jews and Judaism
Star of David
Etymology·
Who is a Jew?
Jewish peoplehood
Jewish identity
Religion[show]
The Essenes (in Modern but not in Ancient Hebrew: אִסִּיִים, Isiyim; Greek: Εσσήνοι, Εσσαίοι, or Οσσαίοι, Essḗnoi, Essaíoi, Ossaíoi) were a sect of Second Temple Judaism that flourished from the 2nd century BCE to the 1st century CE which some scholars claim seceded from the Zadokite priests.[1] Being much fewer in number than the Pharisees and the Sadducees (the other two major sects at the time), the Essenes lived in various cities but congregated in communal life dedicated to asceticism, voluntary poverty, daily immersion, and abstinence from worldly pleasures, including (for some groups) celibacy. Many separate but related religious groups of that era shared similar mystic, eschatological, messianic, and ascetic beliefs. These groups are collectively referred to by various scholars as the "Essenes." Josephus records that Essenes existed in large numbers, and thousands lived throughout Roman Judæa.
The Essenes have gained fame in modern times as a result of the discovery of an extensive group of religious documents known as the Dead Sea Scrolls, which are commonly believed to be Essenes' library—although there is no proof that the Essenes wrote them. These documents include preserved multiple copies of the Hebrew Bible untouched from as early as 300 BCE until their discovery in 1946. Some scholars, however, dispute the notion that the Essenes wrote the Dead Sea Scrolls.[2] Rachel Elior questions even the existence of the Essenes.[3][4][5]
The first reference is by the Roman writer Pliny the Elder (died c. 79 CE) in his Natural History.[6] Pliny relates in a few lines that the Essenes do not marry, possess no money, and had existed for thousands of generations. Unlike Philo, who did not mention any particular geographical location of the Essenes other than the whole land of Israel, Pliny places them in Ein Gedi, next to the Dead Sea.
A little later Josephus gave a detailed account of the Essenes in The Jewish War (c. 75 CE), with a shorter description in Antiquities of the Jews (c. 94 CE) and The Life of Flavius Josephus (c. 97 CE). Claiming first hand knowledge, he lists the Essenoi as one of the three sects of Jewish philosophy[7] alongside the Pharisees and the Sadducees. He relates the same information concerning piety, celibacy, the absence of personal property and of money, the belief in communality and commitment to a strict observance of Sabbath. He further adds that the Essenes ritually immersed in water every morning, ate together after prayer, devoted themselves to charity and benevolence, forbade the expression of anger, studied the books of the elders, preserved secrets, and were very mindful of the names of the angels kept in their sacred writings.
CATHOLIC ENCYCLOPEDIA: Essenes - New Advent
www.newadvent.org › Catholic Encyclopedia › E
One of three leading Jewish sects mentioned by Josephus as flourishing in the second century B.C., the others being the Pharisees and the Sadducees.
ESSENES
3 |
THE |
33 |
15 |
6 |
7 |
ESSENES |
86 |
23 |
5 |
10 |
First Total |
|
|
|
1+0 |
Add to Reduce |
1+1+9 |
3+8 |
1+1 |
1 |
Second Total |
|
|
|
|
Reduce to Deduce |
1+1 |
1+1 |
- |
|
Essence of Number |
|
|
|
- |
- |
|
|
|
ESSENES |
|
|
|
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
N |
14 |
5 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
E |
= |
5 |
|
|
ESSENES |
|
|
|
- |
- |
- |
- |
- |
- |
8+6 |
5+0 |
2+3 |
E |
= |
5 |
|
7 |
ESSENES- |
|
5 |
5 |
- |
- |
- |
- |
- |
- |
1+4 |
- |
- |
E |
= |
5 |
|
7 |
ESSENES- |
|
5 |
5 |
T |
= |
2 |
|
|
THE |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
E |
= |
5 |
- |
- |
ESSENES |
- |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
2 |
S+S |
38 |
20 |
2 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
N |
14 |
5 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
E |
= |
5 |
|
|
ESSENES |
|
|
|
- |
- |
- |
- |
- |
- |
8+6 |
5+0 |
2+3 |
E |
= |
5 |
|
7 |
ESSENES |
|
5 |
5 |
- |
- |
- |
- |
- |
- |
1+4 |
- |
- |
E |
= |
5 |
|
7 |
ESSENES |
|
5 |
5 |
T |
= |
2 |
|
|
THE |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
E |
= |
5 |
- |
- |
ESSENES |
- |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
6 |
SENSES |
81 |
18 |
9 |
E |
= |
5 |
|
|
ESSENES |
|
|
|
- |
- |
- |
- |
- |
- |
8+6 |
2+3 |
1+4 |
E |
= |
5 |
|
7 |
ESSENES |
|
5 |
5 |
- |
- |
- |
- |
- |
- |
1+4 |
- |
- |
E |
= |
5 |
|
7 |
ESSENES |
|
5 |
5 |
7 |
ESSENES |
86 |
23 |
5 |
|
|
- |
|
|
|
|
- |
|
|
7 |
ESSENCE |
|
|
|
T |
= |
2 |
|
|
THE |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
E |
= |
5 |
- |
7 |
ESSENCE |
- |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
- |
- |
- |
- |
1 |
S |
19 |
10 |
1 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
N |
14 |
5 |
5 |
- |
- |
- |
- |
1 |
C |
3 |
3 |
3 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
E |
= |
5 |
|
7 |
ESSENCE |
|
|
|
- |
- |
- |
- |
- |
- |
7+0 |
4+3 |
2+5 |
E |
= |
5 |
|
7 |
ESSENCE |
|
7 |
7 |
T |
= |
2 |
|
|
THE |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
E |
= |
5 |
- |
7 |
ESSENCE |
- |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
S+S+C |
41 |
23 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
N |
14 |
5 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
E |
= |
5 |
|
7 |
ESSENCE |
|
|
|
- |
- |
- |
- |
- |
- |
7+0 |
4+3 |
2+5 |
E |
= |
5 |
|
7 |
ESSENCE |
|
7 |
7 |
8 |
|
99 |
45 |
|
8 |
|
94 |
40 |
|
16 |
First Total |
|
|
|
1+6 |
Add to Reduce |
1+9+3 |
8+5 |
1+3 |
7 |
Second Total |
|
|
|
8 |
|
94 |
40 |
|
|
Essence of Number |
|
|
|
|
ESOTERIC |
|
|
|
|
E |
5 |
5 |
|
|
S |
19 |
10 |
|
|
O |
15 |
6 |
|
|
T |
20 |
2 |
|
|
E |
5 |
5 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C |
3 |
3 |
|
8 |
|
94 |
49 |
|
|
|
9+4 |
4+9 |
4+0 |
8 |
|
13 |
13 |
|
|
|
1+3 |
1+3 |
|
8 |
|
4 |
4 |
|
|
ESOTERIC |
|
|
|
|
E |
5 |
5 |
|
|
SOT |
54 |
18 |
|
|
E |
5 |
5 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C |
3 |
3 |
|
8 |
|
94 |
49 |
|
|
|
9+4 |
4+9 |
4+0 |
8 |
|
13 |
13 |
|
|
|
1+3 |
1+3 |
|
8 |
|
4 |
4 |
|
|
ESOTERIC |
|
|
|
|
ESOTE |
64 |
28 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C |
3 |
3 |
|
8 |
|
94 |
49 |
|
|
|
9+4 |
4+9 |
4+0 |
8 |
|
13 |
13 |
|
|
|
1+3 |
1+3 |
|
8 |
|
4 |
4 |
|
|
ESOTERIC |
|
|
|
|
I |
9 |
9 |
|
|
SECRET |
70 |
34 |
|
|
O |
15 |
6 |
|
8 |
|
94 |
49 |
|
|
|
9+4 |
4+9 |
2+2 |
8 |
|
13 |
13 |
|
|
|
1+3 |
1+3 |
|
8 |
|
4 |
4 |
|

|
ESOTERIC |
|
|
|
|
O |
15 |
6 |
|
|
SECRET |
70 |
34 |
|
|
I |
9 |
9 |
|
8 |
|
94 |
49 |
|
|
|
9+4 |
4+9 |
2+2 |
8 |
|
13 |
13 |
|
|
|
1+3 |
1+3 |
|
8 |
|
4 |
4 |
|
P |
= |
|
|
7 |
PYRAMID |
86 |
41 |
5 |
P |
= |
|
|
7 |
PHARAOH |
67 |
40 |
4 |
- |
- |
14 |
|
14 |
Add to Reduce |
153 |
81 |
9 |
- |
- |
1+4 |
- |
1+4 |
Reduce to Deduce |
1+5+3 |
8+1 |
1+8 |
- |
- |
5 |
|
5 |
Essence of Number |
9 |
9 |
9 |

T |
= |
2 |
|
3 |
THE |
33 |
15 |
6 |
G |
= |
7 |
|
5 |
GREAT |
51 |
24 |
6 |
P |
= |
7 |
|
7 |
PYRAMID |
86 |
41 |
5 |
O |
= |
6 |
|
2 |
OF |
21 |
12 |
3 |
G |
= |
7 |
|
4 |
GIZA |
43 |
25 |
7 |
|
|
|
|
21 |
First Total |
|
|
|
|
|
2+9 |
|
2+1 |
Add to Reduce |
2+3+4 |
1+1+7 |
2+7 |
|
|
|
|
3 |
Second Total |
|
|
|
|
|
1+1 |
|
|
Reduce to Deduce |
- |
- |
- |
|
|
|
|
|
Essence of Number |
|
|
|


- |
- |
- |
|
- |
OSIRIS |
- |
|
- |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
S |
= |
1 |
- |
3 |
SOS |
53 |
26 |
8 |
- |
- |
28 |
|
6 |
OSIRIS |
|
|
|
- |
- |
2+8 |
- |
- |
- |
8+9 |
5+3 |
3+5 |
- |
- |
10 |
- |
6 |
OSIRIS |
|
|
|
- |
- |
1+0 |
- |
- |
- |
1+7 |
- |
- |
- |
- |
|
- |
6 |
OSIRIS |
|
|
|
- |
- |
- |
|
- |
OSIRIS |
- |
|
- |
S |
= |
1 |
- |
3 |
SO |
34 |
16 |
7 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
IS |
28 |
10 |
1 |
- |
- |
28 |
|
6 |
OSIRIS |
|
|
|
- |
- |
2+8 |
- |
- |
- |
8+9 |
5+3 |
3+5 |
- |
- |
10 |
- |
6 |
OSIRIS |
|
|
|
- |
- |
1+0 |
- |
- |
- |
1+7 |
- |
- |
- |
- |
|
- |
6 |
OSIRIS |
|
|
|

- |
EGYPT |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
|
- |
5 |
1 |
G |
7 |
7 |
7 |
- |
7 |
- |
1 |
Y |
25 |
7 |
7 |
- |
7 |
- |
1 |
P |
16 |
7 |
7 |
- |
7 |
- |
1 |
T |
20 |
2 |
2 |
|
- |
2 |
5 |
EGYPT |
73 |
28 |
28 |
- |
21 |
7 |
|
- |
7+3 |
2+8 |
2+8 |
- |
2+1 |
- |
5 |
EGYPT |
10 |
10 |
10 |
|
3 |
7 |
|
- |
1+0 |
1+0 |
1+0 |
- |
- |
- |
5 |
EGYPT |
1 |
7 |
7 |
|
3 |
7 |
SR intro Pentauch
https://www.suscopts.org › srintropentateuch
B. The term "Pentateuch" comes from the Greek term pent-teuchos meaning "five- volumes (book) after the Jewish designation, "the five-fifths of the law". C. The ...
Pentateuch
the first five books of the Old Testament (Genesis, Exodus, Leviticus, Numbers, and Deuteronomy). Traditionally ascribed to Moses, it is now held by scholars to be a compilation from texts of the 9th to 5th centuries bc.Jewish name Torah.
What is the Greek word for pentateuch?
The Greek word Pentateuch (“five books”) refers to the first five books of the Bible, collectively to Genesis, Exodus, Leviticus, Numbers, and Deuteronomy. To a Jew, these five books are also known collectively as Torah, or The Torah. Traditionally, it is understood that the Pentateuch was written by Moses,...
What Is the Pentateuch in the Bible?
https://www.biblestudytools.com/bible-study/topical-studies/what...
23/02/2019 · The Greek word Pentateuch (“five books”) refers to the first five books of the Bible, collectively to Genesis, Exodus, Leviticus, Numbers, and Deuteronomy. To a Jew, these five books are also known collectively as Torah, or The Torah.
What is the Pentateuch? | GotQuestions.org
https://www.gotquestions.org/Pentateuch.html
02/01/2020 · The word Pentateuch comes from a combination of the Greek word penta, meaning “five” and teuchos, which can be translated “scroll.” Therefore, it simply refers to the five scrolls that make up the first of three divisions of the Jewish canon.
SR intro Pentauch
https://www.suscopts.org › srintropentateuch
B. The term "Pentateuch" comes from the Greek term pent-teuchos meaning "five- volumes (book) after the Jewish designation, "the five-fifths of the law". C. The ...
If you've never heard of the Five Books of Moses (not actually composed by Moses; people who believe in divine revelation see him as more secretary than author), you've heard of the Torah and the Pentateuch, the Hebrew and Greek names, respectively, for the first five books of the Hebrew Bible: Genesis, Exodus
P |
= |
7 |
- |
9 |
PENTATEUCH |
113 |
41 |
5 |
|
PENTATEUCH |
|
|
|
1 |
|
16 |
7 |
|
1 |
|
5 |
5 |
|
1 |
N |
14 |
5 |
5 |
3 |
|
41 |
5 |
|
1 |
|
5 |
5 |
|
3 |
|
32 |
5 |
|
|
PENTATEUCH |
|
|
|
- |
|
1+1+3 |
4+1 |
4+1 |
|
PENTATEUCH |
|
|
|
The unexamined life is not worth living - Wikipedia
https://en.wikipedia.org › wiki › The_unexamined_life...
This statement relates to Socrates' understanding and attitude towards death and his commitment to fulfill his goal of investigating and understanding the ...
Rationale · Interpretation
"The unexamined life is not worth living" (Ancient Greek: ... is a famous dictum apparently uttered by Socrates at his trial for impiety and corrupting youth, for which he was subsequently sentenced to death, as described in Plato's Apology (38a5–6).
RATIONALE
This statement relates to Socrates' understanding and attitude towards death and his commitment to fulfill his goal of investigating and understanding the statement of the Pythia (i.e. that there was no one wiser than Socrates). Socrates understood the Pythia's response to Chaerephon's question as a communication from the god Apollo and this became Socrates's prime directive, his raison d'etre. For Socrates, to be separated from elenchus by exile (preventing him from investigating the statement) was therefore a fate worse than death. Since Socrates was religious and trusted his religious experiences, such as his guiding daimonic voice, he accordingly preferred to continue to seek the truth to the answer to his question, in the after-life, than live a life not identifying the answer on earth.[1]
Meaning?[edit]
The words were supposedly spoken by Socrates at his trial after he chose death rather than exile. They represent (in modern terms) the noble choice, that is, the choice of death in the face of an alternative.[2]
Interpretation?[edit]
See also: Trial of Socrates § Interpretations of the trial of Socrates
Socrates believed that philosophy – the love of wisdom – was the most important pursuit above all else. For some, he exemplifies more than anyone else in history the pursuit of wisdom through questioning and logical argument, by examining and by thinking. His 'examination' of life in this way spilled out into the lives of others, such that they began their own 'examination' of life, but he knew they would all die one day, as saying that a life without philosophy – an 'unexamined' life – was not worth living.[3][4]
S |
= |
1 |
|
|
SOCRATES |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
U |
= |
3 |
- |
10 |
UNEXAMINED |
110 |
47 |
2 |
L |
= |
3 |
- |
4 |
LIFE |
32 |
23 |
5 |
I |
= |
9 |
- |
2 |
IS |
28 |
10 |
1 |
N |
= |
5 |
- |
3 |
NOT |
49 |
13 |
4 |
W |
= |
5 |
- |
5 |
WORTH |
84 |
30 |
3 |
L |
= |
3 |
- |
6 |
LIVING |
73 |
37 |
1 |
- |
- |
30 |
- |
33 |
First Total |
|
|
|
- |
- |
3+0 |
- |
3+3 |
Add to Reduce |
4+0+9 |
1+7+5 |
3+1 |
- |
- |
3 |
- |
6 |
Second Total |
|
|
|
- |
- |
|
- |
|
Reduce to Deduce |
1+3 |
1+3 |
- |
- |
- |
|
- |
|
Essence of Number |
|
|
|
SOCRATES THE UNEXAMINED LIFE IS NOT WORTH LIVING
S |
= |
1 |
|
|
SOCRATES |
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
U |
= |
3 |
- |
10 |
UNEXAMINED |
110 |
47 |
2 |
L |
= |
3 |
- |
4 |
LIFE |
32 |
23 |
5 |
I |
= |
9 |
- |
2 |
IS |
28 |
10 |
1 |
N |
= |
5 |
- |
3 |
NOT |
49 |
13 |
4 |
W |
= |
5 |
- |
5 |
WORTH |
84 |
30 |
3 |
L |
= |
3 |
- |
6 |
LIVING |
73 |
37 |
1 |
- |
- |
31 |
- |
41 |
First Total |
|
|
|
- |
- |
3+1 |
- |
4+1 |
Add to Reduce |
5+0+9 |
2+2+1 |
2+3 |
- |
- |
4 |
- |
5 |
Second Total |
|
|
|
- |
- |
|
- |
|
Reduce to Deduce |
1+4 |
- |
|
- |
- |
|
- |
|
Essence of Number |
|
|
|
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
A |
= |
1 |
- |
2 |
AM |
14 |
14 |
5 |
- |
- |
- |
- |
- |
RENEWED |
- |
- |
- |
- |
- |
- |
- |
1 |
R |
18 |
9 |
9 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
N |
14 |
5 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
W |
23 |
5 |
5 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
- |
- |
- |
- |
1 |
D |
4 |
4 |
4 |
R |
= |
9 |
- |
7 |
RENEWED |
|
|
|
- |
- |
- |
- |
- |
- |
7+4 |
3+8 |
3+8 |
- |
- |
9 |
- |
|
RENEWED |
|
|
|
- |
- |
- |
- |
- |
- |
1+1 |
1+1 |
1+1 |
- |
- |
9 |
- |
|
RENEWED |
|
|
|
|
REDEEMER |
- |
- |
- |
|
R |
18 |
9 |
|
- |
E |
5 |
5 |
5 |
- |
D |
4 |
4 |
4 |
- |
E |
5 |
5 |
5 |
- |
E |
5 |
5 |
5 |
- |
M |
13 |
4 |
4 |
- |
E |
5 |
5 |
5 |
|
R |
18 |
9 |
|
8 |
REDEEMER |
73 |
46 |
41 |
|
|
7+3 |
4+6 |
4+1 |
8 |
REDEEMER |
10 |
10 |
5 |
|
|
1+0 |
- |
- |
8 |
REDEEMER |
1 |
1 |
1 |
|
REDEEMER |
- |
- |
- |
|
R |
18 |
9 |
|
|
E+D |
9 |
9 |
|
- |
E |
5 |
5 |
5 |
- |
E |
5 |
5 |
5 |
|
M+E |
18 |
9 |
|
|
R |
18 |
9 |
|
8 |
REDEEMER |
73 |
46 |
41 |
|
|
7+3 |
4+6 |
4+1 |
8 |
REDEEMER |
10 |
10 |
5 |
|
|
1+0 |
- |
- |
8 |
REDEEMER |
1 |
1 |
1 |
J |
= |
1 |
- |
6 |
JOSEPH |
73 |
28 |
1 |
J |
= |
1 |
- |
5 |
JESUS |
74 |
11 |
2 |
M |
= |
4 |
- |
4 |
MARY |
57 |
21 |
3 |
- |
- |
6 |
- |
|
- |
|
|
|
- |
- |
- |
- |
1+5 |
- |
2+0+4 |
6+0 |
- |
- |
- |
- |
- |
|
|
|
|
|
- |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
6 |
JOSEPH |
1 |
6+1 |
7 |
- |
- |
- |
- |
5 |
JESUS |
2 |
5+2 |
7 |
- |
- |
- |
- |
4 |
MARY |
3 |
4+3 |
7 |
RE THE HOLY FAMILY
REMEMBER THE HOLY SEVEN
THE ROOT NUMBER OF THE 6 LETTERED JOSEPH = 1 (6+1) = 7
THE ROOT NUMBER OF THE 5 LETTERED JESUS = 2 (2+5) = 7
THE ROOT NUMBER OF THE 4 LETTERED MARY = 3 (4+3) = 7
J |
= |
1 |
- |
6 |
JOSEPH |
73 |
28 |
1 |
J |
= |
1 |
- |
5 |
JESUS |
74 |
11 |
2 |
M |
= |
4 |
- |
4 |
MARY |
57 |
21 |
3 |
- |
- |
6 |
- |
|
- |
|
|
|
- |
- |
- |
- |
1+5 |
- |
2+0+4 |
6+0 |
- |
- |
- |
- |
- |
|
|
|
|
|
- |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
6 |
JOSEPH |
1 |
6+1 |
7 |
- |
- |
- |
- |
5 |
JESUS |
2 |
5+2 |
7 |
- |
- |
- |
- |
4 |
MARY |
3 |
4+3 |
7 |
- |
EGYPT |
- |
- |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
|
- |
5 |
1 |
G |
7 |
7 |
7 |
- |
7 |
- |
1 |
Y |
25 |
7 |
7 |
- |
7 |
- |
1 |
P |
16 |
7 |
7 |
- |
7 |
- |
1 |
T |
20 |
2 |
2 |
|
- |
2 |
5 |
EGYPT |
73 |
28 |
28 |
- |
21 |
7 |
|
- |
7+3 |
2+8 |
2+8 |
- |
2+1 |
- |
5 |
EGYPT |
10 |
10 |
10 |
|
3 |
7 |
|
- |
1+0 |
1+0 |
1+0 |
- |
- |
- |
5 |
EGYPT |
1 |
7 |
7 |
|
3 |
7 |


- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
- |
- |
1+0 |
- |
- |
|
1+1+3 |
5+0 |
2+3 |
- |
- |
1 |
|
9 |
THE SUN GOD |
5 |
5 |
5 |
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
3 |
|
33 |
15 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
3 |
|
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
3 |
|
26 |
17 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
10 |
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
1+0 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+1+3 |
5+0 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
THE SUN GOD |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
10 |
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
1+0 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+1+3 |
5+0 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
THE SUN GOD |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
9 |
THE SUN GOD |
- |
- |
- |
|
|
|
|
|
10 |
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
1+0 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
- |
9 |
THE SUN GOD |
113 |
50 |
23 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+1+3 |
5+0 |
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
THE SUN GOD |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
Solar deity - Wikipedia
https://en.wikipedia.org › wiki › Solar_deity
A solar deity (also sun goddess or sun god) is a sky deity who represents the Sun, or an aspect of it, usually by its perceived power and strength. Solar deities and Sun worship can be found throughout most of recorded history in various forms.
A solar deity is a god or goddess who represents the Sun, or an aspect of it, usually by its perceived power and strength. Solar deities and Sun worship can be found throughout most of recorded history in various forms.
RE RA RARE RA RE
R |
= |
9 |
- |
4 |
RARE |
- |
- |
- |
- |
- |
- |
- |
1 |
R |
18 |
9 |
9 |
- |
- |
- |
- |
1 |
A |
1 |
1 |
1 |
- |
- |
- |
- |
1 |
R |
18 |
9 |
9 |
- |
- |
- |
- |
1 |
E |
5 |
5 |
5 |
R |
= |
9 |
- |
4 |
RARE |
|
|
|
- |
- |
- |
- |
- |
- |
7+0 |
4+3 |
2+5 |
R |
= |
9 |
- |
4 |
RARE |
|
7 |
7 |
RE RA RARE RA RE
Re | Description, Meaning, & Facts | Britannica
https://www.britannica.com › topic
29 Apr 2021 — The sun god Re (Ra), one of the creator gods of ancient Egypt. Judie Anderson/Encyclopædia Britannica, Inc. Originally most solar gods ...
Re, also spelled Ra or Pra, in ancient Egyptian religion, god of the sun and creator god. He was believed to travel across the sky in his solar bark and, during the night, to make his passage in another bark through the underworld, where, in order to be born again for the new day, he had to vanquish the evil serpent Apopis (Apepi). As one of the creator gods, he rose from the ocean of chaos on the primeval hill, creating himself and then in turn engendering eight other gods.
Originally most solar gods had falcon form and were assimilated to Horus. By the 4th dynasty (c. 2575–c. 2465 bce), however, Re had risen to his leading position. Many syncretisms were formed between Re and other gods, producing such names as Re-Harakhty, Amon-Re, Sebek-Re, and Khnum-Re. Aspects of other gods influenced Re himself; his falcon-headed appearance as Re-Harakhty originated through association with Horus. The influence of Re was spread from On (Heliopolis), which was the centre of his worship. From the 4th dynasty, kings held the title “Son of Re,” and “Re” later became part of the throne name they adopted at accession. As the father of Maat, Re was the ultimate source of right and justice in the cosmos.
At Thebes, by the late 11th dynasty (c. 1980 bce), Re was associated with Amon as Amon-Re, who was for more than a millennium the principal god of the pantheon, the “king of the gods,” and the patron of kings. The greatest development of solar religion was during the New Kingdom (1539–c. 1075 bce). The revolutionary worship of the sun disk, Aton, during the abortive Amarna period (1353–1336 bce) was a radical simplification of the cult of the sun. During the New Kingdom, beliefs about Re were harmonized with those concerning Osiris, the ruler of the underworld, with the two gods syncretized in the royal mortuary texts.
RE THE SUN GOD
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
- |
- |
1+9 |
- |
1+1 |
|
1+3+6 |
6+4 |
2+8 |
- |
- |
10 |
|
2 |
THE SUN GOD RE |
10 |
10 |
10 |
- |
- |
1+0 |
- |
- |
|
1+0 |
1+0 |
1+0 |
- |
- |
1 |
|
2 |
RE THE SUN GOD |
1 |
1 |
1 |
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
3 |
|
33 |
15 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
3 |
|
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
3 |
|
26 |
17 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
2 |
|
23 |
14 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1+5 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+6 |
6+4 |
2+8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RE |
10 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RE THE SUN GOD |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
1+5 |
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
6 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+6 |
6+4 |
2+8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RE |
10 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RE THE SUN GOD |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RE |
- |
- |
- |
|
|
|
|
|
1+5 |
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
6 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RE |
23 |
14 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RE THE SUN GOD |
136 |
64 |
28 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+6 |
6+4 |
2+8 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RE |
10 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RE THE SUN GOD |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
RE THE SUN GOD
THE SUN GOD RA
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
- |
- |
1+9 |
- |
1+1 |
|
1+3+2 |
6+0 |
2+4 |
- |
- |
10 |
|
2 |
THE SUN GOD RA |
6 |
6 |
6 |
- |
- |
1+0 |
- |
- |
|
- |
- |
- |
- |
- |
1 |
|
2 |
RA THE SUN GOD |
6 |
6 |
6 |
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
3 |
|
33 |
15 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
3 |
|
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
3 |
|
26 |
17 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
2 |
|
19 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1+5 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+2 |
6+0 |
2+4 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RA |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RA THE SUN GOD |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1+5 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+2 |
6+0 |
2+4 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RA |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RA THE SUN GOD |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
11 |
THE SUN GOD RA |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
|
|
|
|
|
15 |
|
|
|
|
S |
= |
1 |
- |
3 |
SUN |
54 |
18 |
9 |
|
|
|
|
|
1+5 |
|
|
|
|
G |
= |
7 |
- |
3 |
GOD |
26 |
17 |
8 |
|
|
|
|
|
6 |
|
|
|
|
R |
= |
9 |
- |
2 |
RA |
19 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
- |
- |
19 |
- |
11 |
RA THE SUN GOD |
132 |
60 |
24 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+9 |
- |
1+1 |
|
1+3+2 |
6+0 |
2+4 |
|
|
|
|
|
|
|
|
|
|
- |
- |
10 |
|
2 |
THE SUN GOD RA |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+0 |
- |
- |
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
1 |
|
2 |
RA THE SUN GOD |
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|


